Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 39
14.40. Uma bola de 100 g, presa a uma mola com constante elástica de 2,5 N/m, oscila horizontalmente sobre uma mesa sem atrito. Sua velocidade é de 20 cm/s quando x=-5,0 cm.
a. Qual é a amplitude da oscilação?
b. Qual é a aceleração máxima da bola?
c. Qual é a posição da bola quando a aceleração é máxima?
d. Qual é a velocidade da bola quando x=3,0 cm?
Passo 1
A situação que a gente tem é a seguinte:
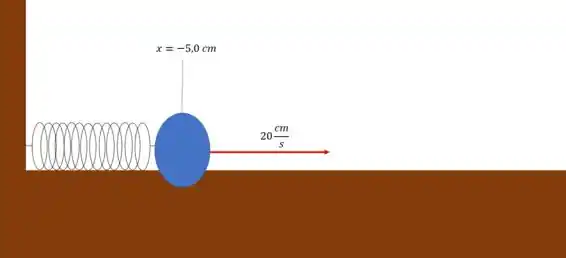
Adotando a direita como sentido positivo.
Bom, essa situação é um movimento harmônico simples.
Vamos começar pelo item (a), calcular a amplitude da oscilação. A gente pode usar a equação
Bom, a gente pode assumir que a posição inicial é e a velocidade inicial é como está na figura. Agora só falta descobrir a velocidade angular. A gente consegue descobrir essa velocidade usando a constante de mola e a massa, que são duas coisas que nos são dadas no enunciado
Vamos substituir os valores
Agora a gente tem tudo para descobrir a amplitude
Vamos substituir os valores
O resultado está em centímetros porque a gente calculou com a posição em e a velocidade em .
Passo 2
Agora vamos para o item (b). A aceleração máxima da bola pode ser calculada assim
A gente chega nessa equação derivando a equação da velocidade do movimento harmônico simples e igualando à 0.
Vamos substituir os valores
Passo 3
Agora o item (c), a posição da bola quando a aceleração é máxima.
A maior aceleração em módulo do movimento harmônico sempre ocorre nas amplitudes. Quando está na amplitude da direita, a bola sofre a maior aceleração para a esquerda, e quando está na amplitude da esquerda acontece o inverso, apesar da velocidade ser nula nesses momentos.
O exercício pede a maior aceleração, então vamos pegar o momento em que o módulo da aceleração é máximo, ou seja, em uma das amplitudes, e a aceleração seja positiva, ou seja, apontando para a direita. Bom, para a aceleração máxima estar apontando para a direita, a bola tem que estar na amplitude da esquerda, ou seja, a menor posição do movimento.
Então ocorre quando . A resposta é
Passo 4
Só falta o item (d) agora. Para achar a velocidade da bola em uma posição qualquer a gente pode usar conservação de energia
Esse maiúsculo é de energia cinética, o minúsculo é a constante da mola.
Bom, vamos pegar o instante 1 como um instante que a gente conhece as condições, o instante que o enunciado descreveu, o da figura que a gente fez. E o segundo instante é o da posição .
A gente tem então
A gente quer descobrir a velocidade no segundo instante, então vamos isola-la
A gente pode cortar , e passar a massa dividindo
Antes de substituir os valores, a gente tem um problema para resolver. Repare que a constante da mola é dada em e a posição e a velocidade são dadas em . A gente tem que deixar tudo na mesma unidade antes de prosseguir, ou seja, colocar tudo que está em em .
Agora a gente pode substituir os valores
Ou ainda
Resposta
Ei, a resposta está no passo a passo :)