Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 14.Exercícios e Problemas - Ex. 6

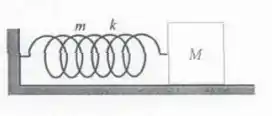
14.5E A mola que compõe o oscilador visto na Figura 14.6 tem massa m . A) Mostre que a mola contribui para a energia cinética do oscilador com um termo 1 6 m v 2 , onde v é a velocidade do bloco. B) Escreva a lagrangeana do sistema.

Passo 1

Belezoca galerinha, a lagrangeana do sistema é dada por:

L = K - V

Onde K é a energia cinética do sistema, enquanto V é a energia potencial. E como se trata de um sistema massa mola, temos que a energia cinética total, vai ser a soma da energia cinética do bloco com a energia cinética da mola. E a malandragem aqui, é que como a mola se deforma e se desloca no espaço, vamos tratar a massa como m / 3 . Dessa maneira, temos que:

K = K 1 + K 2

Sendo K 1 a energia da mola:

K 1 = 1 2 m 3 v 2

K 1 = 1 6 m v ²

Já a energia cinética do bloco é:

K 2 = 1 2 M v 2

De forma que:

K = 1 2 M v 2 + 1 6 m v ²

K = 1 2 v 2 M + m 3

Passo 2

Já a energia potencial, é associado a mola, tal que:

V = 1 2 k x 2

Dessa maneira a lagrangeana é:

L = K - V

L = 1 2 v 2 M + m 3 - 1 2 k x 2

Resposta

  1. Demonstração
  2. L = 1 2 v 2 M + m 3 - 1 2 k x 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma mola de massa desprezível está pendurada no teto com um pequeno objeto preso à extremidade inferior. O objeto é inicialmente mantido em repouso em uma posição y , tal que a mola se encontra no est
12 . Uma esfera de raio r e massa m , sob o efeito da gravidade, rola no interior de uma casca esférica imóvel de raio R . A ) Escreva a lagrangeana do sistema para pequenos deslocamentos da esfera em
9 . (Repetição de problema do Capítulo 13 , Oscilador harmônico.) Ao oscilar forçado pela mola, o cilindro visto na figura 14.9 rola sobre o piso, girando livremente em torno do seu eixo. A ) Escreva
11 . A Figura 14.11 mostra uma esfera de raio r e massa m que rola dentro de um parabolóide. Um corte no plano x y do parabolóide gera uma parábola cuja equação é y = 1 2 C x 2 . A ) Escreva a lagrang
8 . A barra fina vista na Figura 14.8 , cm comprimento l e massa m , oscila como um pêndulo em torno de um eixo à distância b da sua extremidade superior. A ) Escreva a lagrangeana do pêndulo. B ) Cal