Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 69
Dois operários puxam horizontalmente uma pesada caixa, mas um deles exerce o dobro de força do outro. A tração mais forte está direcionada a 25,0º do oeste para o norte, e a resultante dessas duas trações é 350,0 N diretamente no sentido norte. Use componentes de vetores para determinar o módulo de cada uma dessas trações e a direção da tração mais fraca.
Passo 1
E aí, pessoal! 😎
Pra entender melhor a questão, vamos usar a imagem que mostra todo o esquema que ela quer que a gente análise:
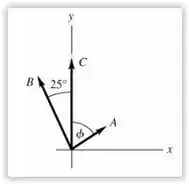
Então a gente tem as seguintes informações: ; , ; ; ; ; e .
Perceba que estamos usando seno para as componentes em e cosseno para as componentes em pois os ângulos dados são em relação a semieixo positivo de .
E agora queremos saber quais os módulos das forças de A e de B e a direção delas através da decomposição de vetores.
Só bora!
Passo 2
Pra achar o valor do ângulo que A faz com o eixo y, vamos usar a soma das componentes em x, já que Cx é igual a 0, o que vai facilitar o nosso cálculo. Hehe.
Agora tiramos o arcsen desse valor pra, assim, encontrar o ângulo:
O fato do ângulo ser negativo significa que ele está crescendo para a direita, como mostra a figura.
Passo 3
Agora que temos o valor de vamos substituí-lo na soma na soma das componentes em y e assim achar o valor de A, e consequentemente o de B.
Como o valor de B é duas vezes o valor de A, pra acha-lo é só multiplicar a intensidade da força de A por 2, e assim temos B = 299,2N.
E acabou!!!! Entendeu tudo? Responde Aí! 😉
Resposta
Módulo de A: 149,6N
Direção de A: Primeiro quadrante, fazendo 57,7 com o eixo y.
Módulo de B: 299,2N
Direção de B: Segundo quadrante, fazendo ângulo de 25 com o eixo y.