Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 71
Você deseja programar o movimento do braço de um robô em uma linha de montagem para se mover no plano xy. Seu primeiro deslocamento é ; seu segundo deslocamento é , cujo módulo é igual a 6,40 cm, formando um ângulo de 63,0°, medido considerando-se uma rotação do eixo +Ox para o eixo -Oy. A resultante dos dois deslocamentos deve também possuir módulo igual a 6,40 cm, porém formando um ângulo de 22,0°, medido considerando-se uma rotação do eixo +Ox para o eixo +Oy. a) Desenhe um diagrama em escala aproximada para estes vetores. b) Ache os componentes de c) Ache o módulo e a direção de .
Passo 1
E aí, pessoal! 👌
Nesse problema temos dois vetores onde foram dados os módulos e os ângulos de um dos vetores e do vetor resultante e nosso objetivo é desenhar o diagrama dos vetores e o vetor resultante e obter os componentes, o modulo e a direção do outro vetor.
Veja só!
Passo 2
A letra (a) pede pra desenhar o diagrama pra esses vetores, então a gente vai posicionar os vetores e de acordo com indicado pelo enunciado e, em seguida, usar a regra do paralelogramo pra estimar a direção e o sentido de , como mostra a figura:
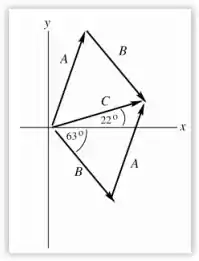
Tranquilo até aqui? 😉
Passo 3
Agora temos que achar as componentes de A. Pra isso vamos usar a soma das componentes em x e em y. Começando por x:
Fazemos, então, em y:
Encontramos as componentes. Agora só falta a última letra.
Só bora!
Passo 4
Agora temos que achar o módulo e a direção de .
Pra achar o módulo, a gente vai usar aquele teorema que a gente tanto ama. O de Pitágoras, é claro! Vamos ver:
Bacana, não é?
Passo 5
Pra achar a direção, precisamos saber o ângulo que faz com o eixo x. Pra isso, vamos usar a nossa querida tangente:
Agora tomamos o arco-tangente desse valor para encontrar o ângulo . Só vamo:
“É TEEETRAA!!!” \O/
Entendeu tudo? Responde Aí! 😎
Resposta
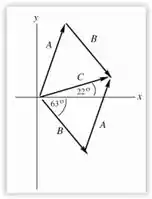
- Módulo: 8,65cm; Ângulo com o eixo x: