Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 3.Exercícios e Problemas - Ex. 30

Carlos corre com velocidade durante 10 minutos. A que distância ao norte de seu ponto de partida Carlos terminará?

Passo 1

Carlos será representado como uma partícula e o modelo de partícula será usado para movimento sob equações cinéticas de aceleração constante.

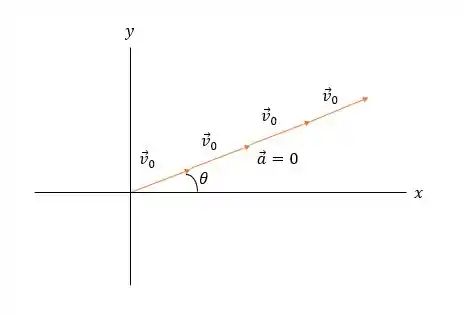
Nós conhecemos: e queremos encontrar .

Passo 2

Carlos corre em velocidade constante sem mudar de direção. A distância total que ele percorre é encontrada na cinemática:

Esse deslocamento fica ao norte do leste, ou do Assim, a posição torna-se

Ou seja, Carlos termina ao norte de sua posição inicial.

Passo 3

A escolha do nosso sistema de coordenadas é tal que o componente do deslocamento é ao longo do leste e o componente está ao longo do norte. O deslocamento de é razoável para Carlos correr em 10 minutos se ele é um atleta.

Resposta

ao norte de sua posição inicial

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ouvindo o ruído de uma serpente, você faz dois deslocamentos rápidos com módulos de 1,8 m e 2,4 m. Usando diagramas (aproximadamente em escala), mostre como esses deslocamentos deveriam ser efetuados

1.70 - Aterrissagem de emergência. Um avião parte do aeroporto de Galisteo e voa a 170 km, a 68º do leste para o norte e depois muda de direção, passando a voar a 230 km e 48º do sul para o leste, faz

1.72 b) Ache o módulo e a direção do vetorS → = C → - A → - B → . Desenhe um diagrama para mostrar como S → é formado com esses três vetores.

1.71 - Você deseja programar o movimento do braço de um robô em uma linha de montagem para se mover no plano xy. Seu primeiro deslocamento é A → ; seu segundo deslocamento é B → , cujo módulo é igual

Para os vetores indicados na Figura 1.27, a) ache o módulo, a direção e o sentido do produto vetorial A → × B → ; b) ache o módulo, a direção e o sentido do produto vetorial B → × A →