Seja e e
- Expresse o vetor em termos de componentes.
- Desenhe um sistema de coordenadas e sobre ele represente os vetores , e .
- Qual é o módulo e qual é a orientação do vetor ?
Passo 1
- Expresse o vetor em termos de componentes.
- Desenhe um sistema de coordenadas e sobre ele represente os vetores , e .
- Qual é o módulo e qual é a orientação do vetor ?
Antes de começarmos a fazer a questão, tenho uma informação que é importante saber: Os vetores unitários , , são vetores que indicam a direção dos eixos e , respectivamente, no plano cartesiano. Então, se eu digo que um vetor , eu quero dizer que sua componente no eixo , , vale 2 e sua componente no eixo , , vale 4, okay?
Então bora.
O vetor é uma soma entre os vetores e , então precisamos saber quem são esses vetores. Para encontrarmos vamos multiplicar cada componente dos vetores e pelo escalar correspondente:
Agora, para obtermos o vetor , basta somarmos as componentes dos vetores e .
Sempre somando, componente com componente e componente com componente , beleza?
Passo 2
Para desenharmos os vetores em um plano cartesiano precisamos saber quais são as componentes e desses vetores. E a questão nos fornece isso em termos dos vetores unitários e .
Para o vetor
Para o vetor
E para o vetor a questão não deu, mas nós encontramos na letra a:
Agora podemos desenhar esses vetores no plano cartesiano:
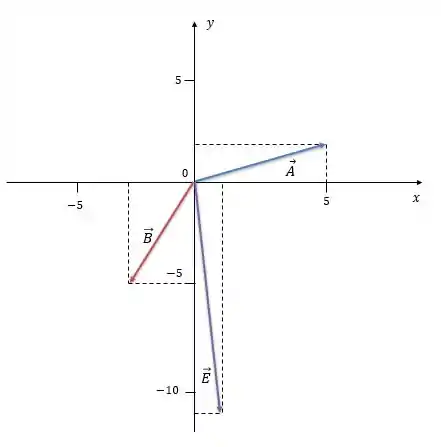
Passo 3
Para essa daqui, precisamos lembrar algumas coisinhas:
O módulo de um vetor é dado por:
Só precisamos saber de mais uma coisinha. Quando a questão está nos pedindo a orientação do vetor, ela está querendo saber qual o ângulo que o vetor faz com um dos eixos da sua escolha, mas lembra que esse eixo deve estar bem especificado beleza?
Da uma olhada aqui:
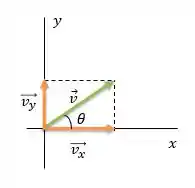
O vetor faz um ângulo acima do semi-eixo positivo. É essa informação que a questão quer saber quando nos pede a orientação.
Mas precisamos saber exatamente quem é esse ângulo . Levando em consideração sempre o ângulo que o vetor faz com o eixo , podemos usar a seguinte fórmula para achar o ângulo:
Foi?? Agora estamos prontos pra resolver
Passo 2
Como já conhecemos as componentes do vetor , vamos calcular o módulo:
Esse vetor faz um ângulo abaixo do semi-eixo positivo:
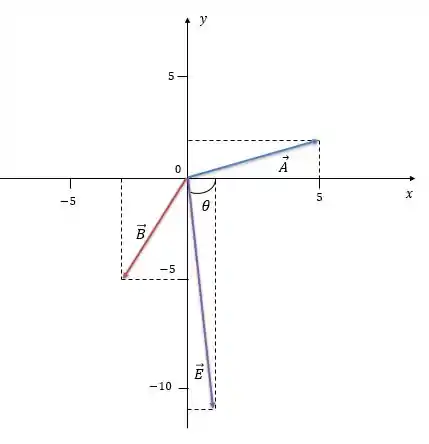
Vamos achar esse ângulo, utilizando a fórmula:
Então, temos que o vetor tem módulo igual a e está à abaixo do semi-eixo positivo.
Resposta
-
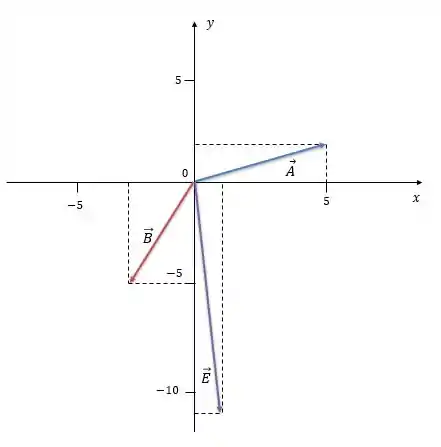
- O vetor tem módulo igual a e está à abaixo do semi-eixo positivo.