Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 1.Problemas - Ex. 86a
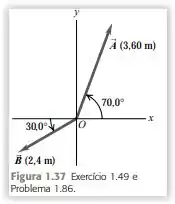
Para os vetores desenhados na Figura 1.37, a) ache o produto escalar
Passo 1
E aí, galerinha!
Nesse problema queremos encontrar o produto escalar dos vetores dados no enunciado...
É até simples achar o produto escalar entre e . É só achar o ângulo entre eles e usar a fórmula:
Então bora!
Passo 2
Primeiro a gente vai ter que achar o ângulo entre os dois vetores. Para isso, vamos ver quantos graus faltam para que o vetor chegue até o eixo +Oy(90°), depois do +Oy até o -Ox(180°) e depois do -Ox até o vetor
Então temos:
Tranquilo até aqui?
Passo 3
Agora que temos o ângulo de 140° e sabemos que A = 3,60m e que B = 2,40m, podemos usar a fórmula do produto escalar:
E conseguimos! \O\ /O/ \O\
Entendeu tudo? Responde Aí!
Resposta
-6,62m²
Exercícios de Livros Relacionados
(a) Seja A → um vetor constante, no plano xy, com sua origem na origem do sistema de coordenadas. Seja r → = x i ^ + y j ^ um vetor do plano xy que satisfaz à relação A → ∙ r → = 1 . Mostre que os pon
Uma partícula se move em um círculo centrado na origem, a magnitude de seu vetor posição r → sendo constante. (a) Derive r → ∙ r → = r 2 = c o n s t a n t e em relação ao tempo, para mostrar que v → ∙
Dois vetores aeb são tais que a + b = a - b . Qual é o ângulo entre aeb ?
Calcule o ângulo entre duas diagonais internas (que passam por dentro) de um cubo, utilizando o produto escalar entre vetores.
O produto escalar de dois vetores unitários perpendiculares deve ser sempre zero? Um corpo tem uma velocidade v → em um dado instante. Interprete fisicamente v → . v → .Uma bola rola para fora de uma