Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 8.Problemas Adicionais - Ex. 134
Uma força conservativa age sobre uma partícula que se move ao longo de um eixo . A figura mostra como a energia potencial associada à força varia com a posição da partícula. (a) Plote no intervalo . (b) A energia mecânica do sistema é de . Plote a energia cinética da partícula diretamente na figura.
Passo 1
(a) Vamos lembrar da relação que dá a força a partir da energia potencial:
Não temos como calcular a derivada em todos os pontos, mas podemos encontrar uma estimativa em alguns pontos, e então fazer uma aproximação para o comportamento nos outros.
Entre os pontos , a energia potencial varia de até , então a inclinação da curva é próxima do seguinte:
No ponto , a derivada do potencial é zero.
No intervalo , a função do potencial é praticamente uma reta, e então a sua derivada é uma constante.
Passo 2
Beleza, então nosso força tem que começar um pouco acima de em , depois cair até zero em , e então descer rapidamente até e prosseguir constante até .
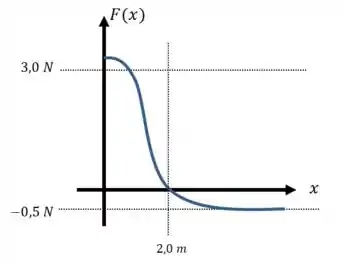
Passo 3
(b) Agora queremos fazer um gráfico da energia cinética diretamente sobre o gráfico que foi dado no enunciado.
Sabemos que a energia mecânica do sistema é . Lembre que a energia mecânica é simplesmente a soma da energia cinética e da enegia potencial:
Então fica fácil plotar a energia cinética a partir do gráfico da energia potencial: é só traçar uma reta na linha e “completar” o desenho:
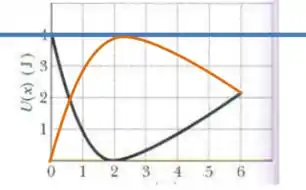
Resposta
(a) Ver gráfico.
(b) Ver gráfico.