Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 28
28. A FIGURA P13.28 mostra três massas. Qual é o módulo e qual é a orientação da força gravitacional resultante sobre a massa de e a massa de ? Determine a orientação por meio de um ângulo horário ou anti-horário com o eixo .
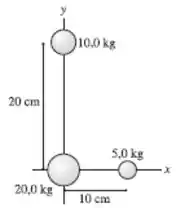
Passo 1
Vamos para cima desse exercício. Primeiro vamos identificar as massas para a gente não se perder.
Lembrando que precisaremos da distância entre a massa de e a de , que por Pitágoras temos que vale . Abaixo temos uma representação pictórica.
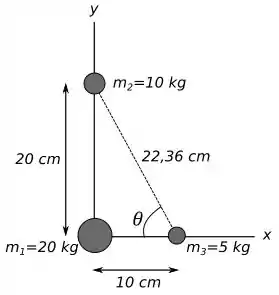
Esse problema tanto no item quanto no item pede a força resultante e sua orientação.
Vamos primeiro discutir a situação de . Ele quer a força resultante em .
Nessa massa temos a ação da força gravitacional de sobre ela na vertical e a força de sobre ela na horizontal .
Com isso a força resultante vai ter duas componentes para achar seu valor basta calcular o módulo dessa força. O ângulo que essa força faz com a vertical pode ser encontrado usando a tangente desse ângulo da seguinte maneira:
Agora para o item ele quer a força resultante em .
Nessa massa temos a ação da força gravitacional de sobre ela na diagonal , logo essa força terá uma componente horizontal e uma vertical com relação ao ângulo , e a força de sobre ela na horizontal .
A força resultante nesse caso também vai ter duas componentes para achar seu valor basta calcular o módulo dessa força. O ângulo que essa força faz com a vertical pode ser encontrado usando a mesmo argumento de .
Vamos adotar o sentido horário como o positivo para a orientação das forças.
Passo 2
Vamos começar com o item .
Primeiro vamos calcular o valor de , temos o seguinte:
Substituindo os valores que conhecemos, temos:
Como essa força está na vertical para cima temos:
Agora vamos calcular o valor de , temos o seguinte:
Substituindo os valores que conhecemos, temos:
Como essa força está na horizontal para direita temos:
Passo 3
Com as informações do passo anterior temos que a força resultante em , temos que:
O módulo dessa força é dado por:
O ângulo de orientação dessa força com a vertical é dado por:
Passo 4
Agora vamos para o item .
Primeiro vamos calcular o valor de , temos o seguinte:
Então temos que:
Como essa força está na horizontal para direita temos:
Agora vamos calcular o valor de , temos o seguinte:
Substituindo os valores que conhecemos, temos:
Temos que essa força é diagonal então decompondo ela nas suas componentes horizontal e vertical, temos:
Mas temos como encontrar os valores de e , da seguinte forma:
E
Então temos que:
Passo 5
Com as informações do passo anterior temos que a força resultante em , temos que:
O módulo dessa força é dado por:
O ângulo de orientação dessa força com a vertical é dado por: