Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 29
29. O pai do Exemplo 8.3 está em pé no topo de uma colina de forma cônica enquanto gira seu filho de em um carrinho preso por uma corda de de comprimento. Os lados da colina são inclinados em. Ele mantém a corda paralela ao solo, e o atrito é desprezível. Que valor de tensão na corda permitirá que o carro gire com as mesmas daquele exemplo?
Passo 1
Opa! Aqui vamos nós de novo!
Olha só! Mesmo com os lados da colina inclinados em , o garoto ainda continuará exercendo um movimento circular descrito pela seguinte imagem abaixo...
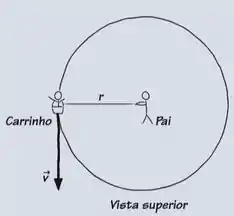
O que vai mudar é o diagrama de corpo livre, uma vez que os lados da colina são inclinados em . Ele vai ter a seguinte cara abaixo;
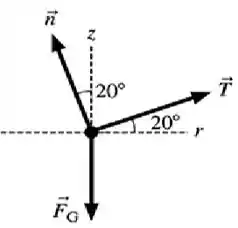
E também sabemos dos seguintes dados...
O raio aqui, também vai ser diferente. Precisamos levar em conta o ângulo de ;
Passo 2
Feito essa parte introdutória, vamos ao que interessa.
Bora aplicar o somatório das forças na direção radial, afinal essa é a direção responsável pelo movimento circular, onde é produzida a resultante centrípeta...
Para determinar a velocidade angular em , basta fazer...
E ficamos com...
Depois, vamos aplicar o somatório das forças na direção . Nessa direção, nosso garoto está em equilíbrio...
Passo 3
Chegamos então, ao seguinte sistema...
Multiplicando a primeira equação por e a segunda por ;
E somando as duas, em seguida...
Quanto a tração :
Esse é o valor da tensão na corda que permitirá que o carro gire com as mesmas daquele exemplo.