Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 30
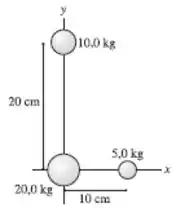
30. Quanto vale a energia potencial gravitacional total das três massas da FIGURA P13.28?
Passo 1
Vamos para cima desse exercício. Primeiro vamos identificar as massas para a gente não se perder.
Lembrando que precisaremos da distância entre a massa de e a de , que por Pitágoras temos que vale . Abaixo temos uma representação pictórica.
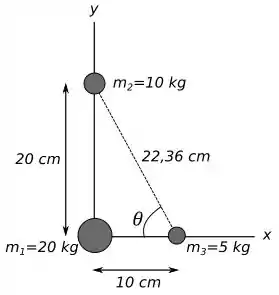
Então galera a energia potencial de um corpo sobre outro é dada pela seguinte equação:
Para calcular a energia potencial total das massas temos que somar a energias potenciais de cada massa em relação a outra. De uma forma clara temos o seguinte:
Onde temos a energia de sobre , a energia de sobre e a energia de sobre as energia dos casos contrários não precisam ser contadas já que elas são iguais. Exemplo:
Passo 2
Vamos então calcular essa energia potencial total, temos o seguinte:
Substituindo as massas que conhecemos, os valores de em metros e o valor de .
Temos o seguinte:
Então temos que: