Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 72

Imagine que seu trabalho para a NASA seja monitorar órbitas de satélites. Um dia, durante uma pesquisa de rotina, você descobre que um satélite de 400 kg, em órbita circular a 1.000 km de altitude, irá colidir com um satélite menor, de 100 kg, que se desloca na mesma órbita, mas em sentido oposto. Conhecendo os detalhes de construção dos dois satélites, você espera que eles se emaranhem, formando uma peça única de detrito espacial. Ao notificar seu chefe dessa colisão iminente, ele pede para você determinar rapidamente se o detrito espacial continuará em órbita ou se colidirá com a Terra. Qual será o resultado de sua análise?

Passo 1

Nesse problema, teremos que nos lembrar do conceito de colisão. Em uma colisão, é importantíssimo lembrar que a quantidade de movimento é conservada. Mas o que é mesmo quantidade de movimento? Quantidade de movimento é a grandeza vetorial dada por:

p → = m v →

onde v → é a velocidade e m a massa da partícula. Além disso, também devemos lembrar do conceito de colisão elástica, parcialmente elástica ou inelástica. No nosso problema, estamos diante de uma colisão inelástica, já que os dois corpos permanecem grudados logo após a colisão!

Também, devemos entender qual deve ser a velocidade de um satélite numa órbita circular. Note o seguinte: a terra atrai qualquer corpo em direção ao seu próprio centro, correto? Essa força irá atuar como uma força centrípeta, obrigando o corpo a percorrer uma trajetória circular. Sendo assim, podemos igualar a força que o planeta faz sobre o corpo com a força centrípeta:

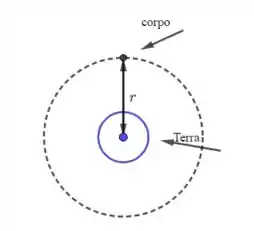
F p l a n e t a = F c e n t r í p e t a G m M r 2 = m v ó r b i t a 2 r v o r b i t a = G M r

onde: G é a constante universal da gravitação; M é a massa do planeta (no caso a Terra) e r é a distância do corpo até o centro da Terra (ver figura abaixo). Note que a velocidade não depende da massa do corpo, somente do planeta. Assim, corpos com massas diferentes, mas com mesmo raio de órbita, terão a mesma velocidade orbital. Legal, né?!

Por fim, quando os satélites colidem, qual será a trajetória do satélite resultante? Sim... a trajetória será elíptica. Vamos então lembrar um pouco sobre trajetórias elípticas.

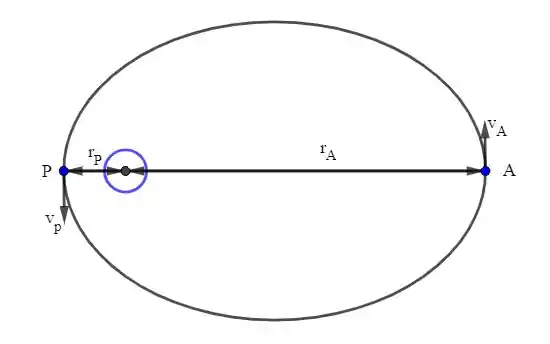
Há dois pontos bastantes notáveis nessa trajetória. Um deles é o ponto A chamado de afélio. Esse é o ponto mais distante possível do centro do planeta; o outro é o ponto P chamado de periélio. Esse é o ponto mais perto do centro do planeta.

A conservação do momento angular nos permite escrever que:

m v A r A = m B v B r B v A r A = v B r B

Outro ponto importante a se destacar é que a energia mecânica (soma da energia potencial com energia cinética) se conserva durante todo o trajeto. Em particular, será conservado entre o ponto A e o ponto P.

Passo 2

Vamos então calcular a velocidade dos corpos imediatamente antes da colisão. Aqui, temos que r = r a i o   d a   t e r r a + a l t i t u d e = 6 370 + 1000 = 7 37 0   k m .

v 1 = v 2 = G M r v = 6,67 × 10 - 11 ⋅ 5,9 8 × 10 24 7 , 37 × 10 6 v = 7 357   m / s

Agora, vamos dar um zoom nos corpos no momento da colisão.

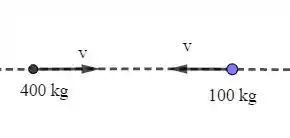
Quando damos o zoom a trajetória que é circular fica parecendo uma retinha... isso ocorre pois estamos desprezando as dimensões dos satélites em comparação com a distância r = 1000   k m . Realmente, 1000 km é muita coisa... Portanto, podemos calcular o momento linear inicial,

p i = 400 v - 100 v p i = 300 v

note que estamos usando a direção para a direita como positiva. Como os dois corpos ficam unidos ao final da colisão, poderemos escrever

p f = m 1 + m 2 u p f = 400 + 100 u p f = 500 u

onde u será a velocidade logo após a colisão. Ora, sabemos que a quantidade de momento permanece inalterada. Sendo assim,

p i = p f 300 v = 500 u u = 300 500 v u = 0,6 v u = 0,6 7357 u = 4414   m / s

Passo 3

Agora que encontramos a velocidade do corpo resultante, vamos analisar se ele vai ou não chocar com a Terra. Para que isso não aconteça, a distância mínima entre o corpo e a Terra (que ocorre no periélio, deve ser maior do que o raio da Terra); entendeu? Se na distância mínima o corpo não se choca com a Terra então em nenhum outro ponto ocorrerá a colisão... faz sentido, não?

Okay, chegamos até aqui. Falta pouco, acredite. Inicialmente, o satélite resultante estará em seu afélio, como mostra a figura a seguir (onde mostra o caso em que não há colisão).

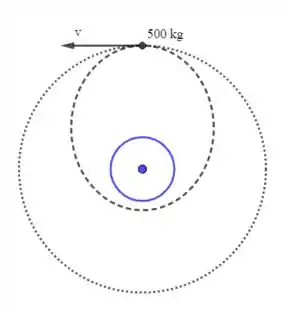
Sendo r P a distância até o periélio, v P a velocidade do satélite no periélio, temos pela conservação do momento angular:

r P v P = r A v A v P = r u r P

Por fim, vamos conservar a energia entre o periélio e o afélio (podemos fazer isso pois a força gravitacional é conservativa). Agora teremos algum trabalho algébrico... acompanhe!

E a f é l i o = E p e r i é l i o - G m M r + 1 2 m u 2 = - G m M r P + 1 2 m v P 2 G M r p - G M r = 1 2 m v P 2 - u 2 G M r - r P r r P = 1 2 m r 2 r P 2 u 2 - u 2 2 G M r - r P r r P = u 2 r 2 - r P 2 r P 2 2 G M r - r P r = u 2 r - r P r + r P r p 2 G M r = u 2 r + r P r P 2 G M r P = r 2 u 2 + r r P u 2 r P 2 G M - r u 2 = r 2 u 2 r P = r 2 u 2 2 G M - r u 2

Substituindo os dados:

r P = 7,37 × 10 6 2 4414 2 2 6,67 × 10 - 11 5,98 × 10 24 - 7,37 × 10 6 4414 2 r P = 1,62 × 10 6   m

Porém, o raio da Terra é de 6,37 × 10 6   m . Então, vemos que r P < r a i o   d a   T e r r a . Sendo assim, ocorrerá a colisão.... :(

Ufa...

Resposta

Ocorrerá a colisão.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula de poeira de um cometa de massa m está a uma distância R do centro da Terra, e a uma distância r do centro da Lua. Se a massa da Terra é M T e a massa da lua é M L , qual é a soma da ene
12.23. O asteroide Dactyl, descoberto em 1993, possui um raio de apenas 700 m e massa aproximadamente igual a 3,6 ⋅ 10 12k g . Use os resultados do Exemplo 12.5 (Seção 12.3) para calcular a velocidade
12.25. Use os resultados do Exemplo 12.5 (Seção 12.3) para calcular a velocidade de escape para uma espaçonave sair a) da superfície de Marte; b) da superfície de Júpiter. Use dados do Apêndice F. c)
12.26. Dez dias após seu lançamento para Marte em dezembro de 1998, a espaçonave Mars Climate Orbiter (massa igual 629 kg) estava a uma distância de 2,87 ⋅ 10 6k m da Terra e se deslocava com velocida
12.24. Massa de um cometa. Em 4 de julho de 2005, a espaçonave Deep Impact da NASA lançou um projetil sobre a superfície do Cometa Tempel 1. Esse cometa tem um diâmetro de cerca de 9,0 km. Observações