Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 77
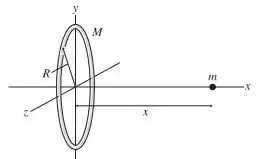
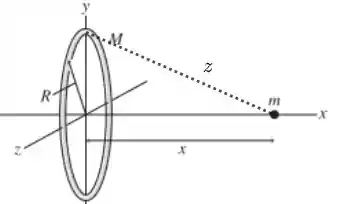
A FIGURA PD13.77 mostra uma partícula de massa m a uma distância x ao longo do eixo de um anel muito fino de massa M e raio R.
a. Calcule a energia potencial gravitacional dessas duas massas.
b. Use o que você sabe sobre a relação entre força e energia potencial para determinar o módulo da força gravitacional exercida sobre m quando ela estiver na posição x.
Passo 1
Queremos determinar a energia potencial entre o anel (que é um corpo extenso) e uma partícula.
Sabemos que a energia potencial entre duas partículas, de massas e é dada por:
onde é a distância entre elas e a constante de gravitação universal.
Podemos pensar em dividir o anel em muitas partículas e então calcular a energia potencial de cada partícula. Logo após, somamos cada uma dessas contribuições de modo a obter a energia potencial total.
A letra b nos pede para obtermos a força . Sabemos que a relação entre a energia potencial e a força é dada por:
Assim, se conhecermos , podemos determinar .
Passo 2
- Para isso, vamos pegar uma partícula de massa no anel. Repare que, como o anel é muito fino, todas as partículas estão a uma mesma distância do anel.
- Vamos agora obter a força . Sabemos que:
Sendo assim, temos que
Pelo teorema de Pitágoras, temos que
Logo,
Note que e são constantes. Sendo assim, podemos integrar a relação acima:
pois .
Passo 3
onde usamos a regra da cadeia.
Resposta
- .