Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 15
|| Um ônibus espacial orbita o Sol à mesma distância que a Terra, mas do lado oposto ao Sol. Uma pequena sonda é lançada do ônibus. Qual é a velocidade mínima que a sonda necessita ter para escapar do Sistema Solar?
Passo 1
Precisamos saber previamente que:
Distancia Terra até o Sol é
Massa do Sol:
E que a velocidade de escape pode ser achada facilmente pela fórmula:
é massa
raio do corpo, ou planeta, se estiver fora da superfície devemos acrescentar essa diferença!
constante gravitacional universal
Então um esquema é:
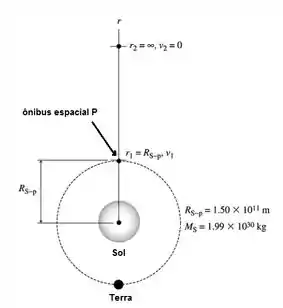
Passo 2
Substituindo os dados:
Resposta
Exercícios de Livros Relacionados
Um corpo é largado, a partir do repouso, de uma altura de 4,0× 10 6m acima da superfície da Terra. Se não existe resistência do ar, qual é sua rapidez ao atingir a Terra?
Calcule a mínima rapidez necessária, em relação à Terra, para que um corpo lançado da superfície da Terra escape do sistema solar. A resposta dependerá da direção do lançamento. Explique a escolha de
Quando calculamos uma rapidez de escape, usualmente o fazemos na suposição de que o corpo lançado está isolado. Isto é, obviamente, geralmente incorreto no sistema solar. Mostre que a rapidez de escap
Um corpo é lançado diretamente para cima da superfície da Terra, com uma rapidez inicial de 4,0k m / s . Qual é a altura máxima que ele alcança?
Uma partícula é lançada da superfície da terra com uma rapidez igual a duas vezes a rapidez de escape. Quando muito distante da terra, qual é a sua rapidez?