Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Problemas - Ex. 57

31.57 Um circuito R-L-C em paralelo está conectado a uma fonte CA com amplitude de voltagem constante igual a V e frequência angular variável ω .

  1. Usando os resultados do Problema 31.54, desenvolva expressões para as amplitudes das correntes I R , I L e I C que passam no resistor, no indutor e no capacitor em função de ω .
  2. Faca um gráfico de I R , I L e I C em função de ω para V =   100   V , R =   200   Ω , L =   2,0   H e C = 0,50   µ F .
  3. Discuta os comportamentos de I L e I C nos limites ω = 0 e ω → ∞ . Explique o comportamento de I L e I C nesses limites.
  4. Calcule a frequência de ressonância (em Hz) do circuito e faça um diagrama de fasores para a frequência de ressonância.
  5. Para a frequência de ressonância, qual é a amplitude da corrente através da fonte?
  6. Para a frequência de ressonância, qual é a amplitude da corrente através do resistor, através do indutor e através do capacitor?

Passo 1

L e t r a   A :

Um protótipo de circuito RLC em paralelo é esse daqui:

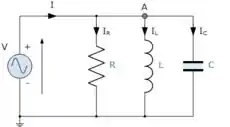
Eu o representei aqui pra ficar mais fácil de perceber que a tensão é a mesma sobre cada elemento, logo a corrente em cima de cada um deles se calcula assim:

I R = V R                 ,                     I L = V X l                       e                     I C = V X c

Onde X representam as reatâncias e que são calculadas através de ômega desse jeito aqui:

I R = V R                 ,                     I L = V ω L                       e                     I C = V 1 / ω C

Então, simplificando as expressões que calculam as correntes em cada elemento são...

I R = V R                 ,                     I L = V ω L                       e                     I C = V ω C

Passo 2

L e t r a   B :

Substituindo-se então os valores do item lembrando-se que 0,5 μ F é na verdade 0,5 ⋅ 10 - 6 F ...

I R = V R                 ,                     I L = V ω L                       e                     I C = V ω C   →

I R = 100 200                 ,                     I L = 100 2 ω                       e                     I C = 100 ω ⋅ 0,5 ⋅ 10 - 6     →

I R = 0,5                 ,                     I L = 50 ω                       e                     I C = 50 ⋅ 10 - 6 ω  

Perceba que I R não depende de ω então será uma constante em, já o segundo trata-se da curva de 1 / x e o terceiro... I C , nada mais é do que uma reta crescente...

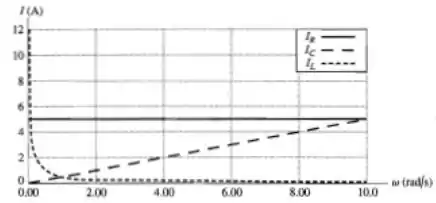
Passo 3

L e t r a   C :

Bem, I L e I C são...

I L = 50 ω                       e                     I C = 50 ⋅ 10 - 6 ω

Em baixas frequências, quando ω = 0 , a corrente que passa no indutor é muito alta, o que faz sentido, pois ω = 0 trata-se de corrente contínua, e em C C , o indutor entra em curto circuito. I C = 0 (o capacitor é um circuito aberto).

Já em altas frequências ( ω → ∞ ) a corrente no indutor cai a 0 enquanto que a do capacitor tende ao infinito, afinal inverte a situação.

Passo 4

L e t r a   D :

A frequência de ressonância do circuito RLC paralelo é...

f = 1 2 π L C   →

Substituindo os valores...

f = 1 2 π 2 ⋅ 0,5 ⋅ 10 - 6 =

159,15   H z

Na frequência de ressonância...

I L = I C =

50 ω = 50 1 L C =

0,05 A

Lembre-se, no indutor ela etsá atrasada 90 ° e no capacitor adiantada de 90 ° . Enquanto que a corrente que passa pelo resistor é de...

I R = 0,5

E ela tem ângulo 0 ° (ela está em fase com a tensão)...

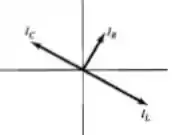
Passo 5

L e t r a   E :

Na frequência de ressonância de um circuito RLC paralelo, a corrente da fonte é a mesma do resistor:

I = I R = 0,5 A

Passo 6

L e t r a   F :

Através do resistor é de 0,5 A e as que passam pelo capacito e indutor, como já vimos tem a mesma amplitude, mas fases opostas. A amplitude delas são de...

I C = I L = 0,05 A

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um resistor e um indutor estão conectados em paralelo com uma fonte de tensão ac ideal cuja saída é dada por ε = ε m a x cos ⁡ ω t como mostrado na figura 29-32. Mostre que (a) a corrente no resistor
Uma bobina com resistência R e indutância L tem um fator de potência igual a 0,866 quando funcionando a 60H z . Qual será o fator de potência da bobina se ela estiver funcionando a 240H z ?
Uma linha de transmissão com dois condutores conduz simultaneamente uma superposição de dois sinais de tensãod e tal forma que a ddp entre os dois condutores é dada por V = V 1 + V 2 , onde V 1 = 10 V
Uma bobina está conectada a uma linha de 120V rms a 60Hz. A potência média fornecida para a bobina é 60 W e a corrente rms é 1,5 A. Determina (a) o fator de potência, (b) a resistência da bobina e (c)
Um capacitor de 5 μ F é carregado a 30 V e, então, é conectado a um indutor ideal de 10m H . (a) Quanta energia é armazenada no sistema? (b) Qual é a frequência de oscilação do circuito? (c) Qual é a