Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Problemas - Ex. 60

60 - Um circuito R-L-C em série possui R   =   500   Ω , L   =   2,0   H , C   =   0,500   µ F e V =   100   V .

  1. Para ω =   800   r a d / s , calcule V R , V L , V C e ϕ usando um único conjunto de eixos, faça um gráfico de v ,   v R ,     v L   e v C em função do tempo. Inclua dois ciclos de v em seu gráfico.
  2. Repita o item a para ω = 1000   r a d / s .
  3. Repita o item a para ω = 1250   r a d / s .

Passo 1

L e t r a   A :

Ora bolas, para um circuito R L C série, a gente pode encontrar aquelas tensões ali fazendo...

V R = R I ,                   V L = X L I               e                   V C = X C I

Onde a corrente por sua vez é...

I = V R 2 + X L - X C 2

Os X são as reatâncias que a gente pode encontrar fazendo...

X L = ω L         e                 X C = 1 ω C

Então, no caso de ω = 800   r a d / s ...

X L = 800 ⋅ 2         e                 X C = 1 800 ⋅ 0,5 ⋅ 10 - 6     →

X L = 1600 Ω         e                 X C = 2500 Ω     →

Então, a corrente será...

I = 100 500 2 + 1600 - 2500 2 =

0,097 A

E as tensões por sua vez...

V R = R I ,                   V L = X L I               e                   V C = X C I   →

V R = 500 ⋅ 0,097 ,                   V L = 1600 ⋅ 0,097               e                   V C = 2500 ⋅ 0,097   →

V R = 48,5 V ,                   V L = 155,2 V               e                   V C = 242,5 V

Passo 2

Bem, esses daí são os módulos, as tensões v no domínio do tempo de cada um deles será: A da fonte:

v = 100 cos ⁡ ω t =

100 cos ⁡ 800 t

Sobre o resistor...

v R = 48,5 cos ⁡ 800 t

Sobre o capacitor (lembrando que a tensão dele está 90 ° atrasada em relação a tensão da fonte):

v C = 242,5 cos ⁡ 800 t + 90 °

Já o indutor...

v L = 155,2 cos ⁡ 800 t - 90 °

Desenhando esses cossenos todos juntos...

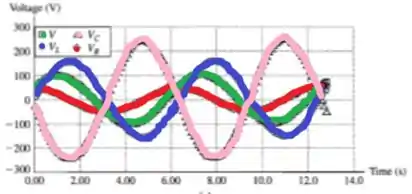
Passo 3

L e t r a   B :

Repetindo os cálculos, mas dessa vez para ω = 1000   r a d / s ...

V R = R I ,                   V L = X L I               e                   V C = X C I

Onde a corrente por sua vez é...

I = V R 2 + X L - X C 2

Os X são as reatâncias que a gente pode encontrar fazendo...

X L = ω L         e                 X C = 1 ω C

Então, no caso de ω = 1000   r a d / s ...

X L = 1000 ⋅ 2         e                 X C = 1 1000 ⋅ 0,5 ⋅ 10 - 6     →

X L = 2000 Ω         e                 X C = 2000 Ω     →

Então, a corrente será...

I = 100 500 2 + 2000 - 2000 2 =

0,2 A

E as tensões por sua vez...

V R = R I ,                   V L = X L I               e                   V C = X C I   →

V R = 100 V ,                   V L = 400               e                   V C = 400 V  

Passo 4

Bem, esses daí são os módulos, as tensões v no domínio do tempo de cada um deles será: A da fonte:

v = 100 cos ⁡ ω t =

100 cos ⁡ 1000 t

Sobre o resistor...

v R = 100 cos ⁡ 1000 t

Sobre o capacitor (lembrando que a tensão dele está 90 ° atrasada em relação a tensão da fonte):

v C = 400 cos ⁡ 1000 t + 90 °

Já o indutor...

v L = 400 cos ⁡ 1000 t - 90 °

Desenhando esses cossenos todos juntos...

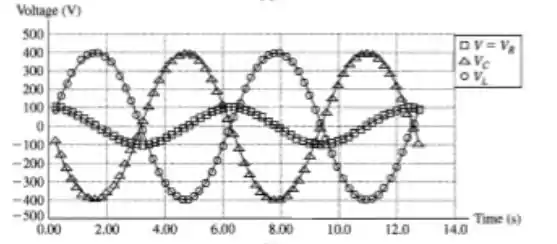
Passo 5

Repetindo os cálculos, mas dessa vez para ω = 1250   r a d / s ...

V R = R I ,                   V L = X L I               e                   V C = X C I

Onde a corrente por sua vez é...

I = V R 2 + X L - X C 2

Os X são as reatâncias que a gente pode encontrar fazendo...

X L = ω L         e                 X C = 1 ω C

Então, no caso de ω = 1250 r a d / s ...

X L = 1250 ⋅ 2         e                 X C = 1 1250 ⋅ 0,5 ⋅ 10 - 6     →

X L = 2500 Ω         e                 X C = 1600 Ω     →

Então, a corrente será...

I = 100 500 2 + 2500 - 1600 2 =

0,097 A

E as tensões por sua vez...

V R = R I ,                   V L = X L I               e                   V C = X C I   →

V R = 500 ⋅ 0,097 ,                   V L = 2500 ⋅ 0,097               e                   V C = 1600 ⋅ 0,097   →

V R = 48,5 V ,                   V L = 242,5 V               e                   V C = 155,2 V

Passo 6

Bem, esses daí são os módulos, as tensões v no domínio do tempo de cada um deles será: A da fonte:

v = 100 cos ⁡ ω t =

100 cos ⁡ 1250 t

Sobre o resistor...

v R = 48,5 cos ⁡ 1250 t

Sobre o capacitor (lembrando que a tensão dele está 90 ° atrasada em relação a tensão da fonte):

v C = 155,2 cos ⁡ 1250 + 90 °

Já o indutor...

v L = 242,5 cos ⁡ 1250 t - 90 °

Desenhando esses cossenos todos juntos...

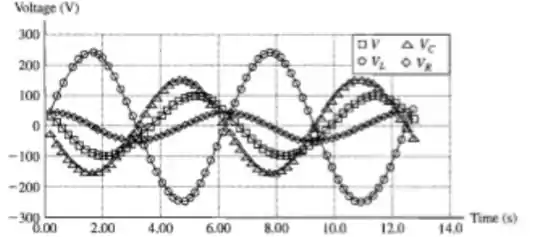
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verdadeiro ou falso: ( a ) Um circuito R L C em série forçado que tem um alto fator Q tem uma curva de ressonância estreita. ( b ) Um circuito consiste apenas em um resistor, um indutor e um capacitor
Um circuito contém um resistor e um indutor ideal conectados em série. A queda de tensão rms na combinação em série é 100 V e a queda de tensão rms no indutor é 80 V . Qual é a queda de potencial rms
Uma bobina com resistência de 80 Ω tem uma impedância de 200 Ω quando conectada a uma frequência de 1k H z . Qual a indutância da bobina?
Um circuito consiste em um resistor, um indutor ideal de 1,4 H e um gerador ideal de 60 H z , todos conectados em série. A tensão rms no resistor é de 30 V e a tensão rms no indutor é de 40 V . (a) Qu
Mostre que 1 / √ L C tem unidade de inverso de segundo substituindo as unidades do S I para a indutância e para a capacitância na expressão. (b) Mostre que ω 0 L / R (a expressão para o fator Q ) é ad