Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 33
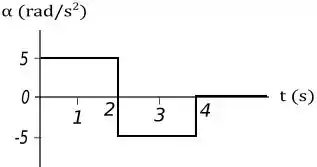
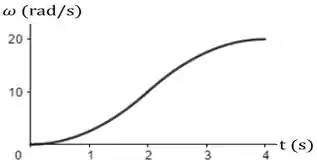
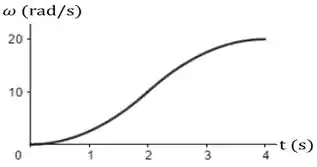
33. A FIGURA EX4.33a mostra a velocidade angular em função do tempo. Desenhe o correspondente gráfico da aceleração angular versus tempo.
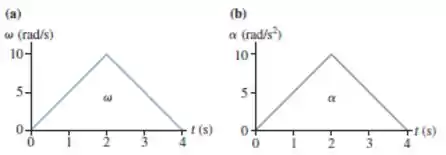
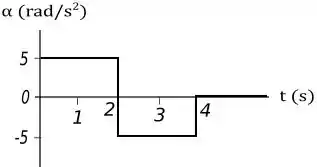
A FIGURA EX.33B mostra a aceleração angular em função do tempo. Desenhe o correspondente gráfico da velocidade angular versus tempo. Considere.
Passo 1
Para fazer o gráfico que é pedido no item primeiro vamos analisar o comportamento do gráfico que temos, pois assim podemos encontrar a aceleração angular, já que:
A partir disso podemos saber a aceleração angular do eixo em um intervalo de tempo.
Para fazer o gráfico da velocidade angular pedido em podemos usar o seguinte:
Assim temos que:
Assim encontramos uma função e podemos montar o gráfico.
Mas para isso precisamos uma função , temos que de até e de até temos um comportamento linear de , logo podemos encontrar a função que define essas duas partes do gráfico assim:
Para a primeira parte, para a segunda temos:
Passo 2
Vamos começar nos dedicando a encontrar o gráfico pedido em , podemos analisar o gráfico do enunciado da seguinte forma:
Temos que de até temos uma variação da velocidade angular de , assim temos que .
De até temos uma variação da velocidade angular de , assim temos que .
Com essa análise temos que o nosso gráfico fica da seguinte forma:
Passo 3
Agora vamos para o item .
Vamos então encontrar a função para de até , temos:
Agora podemos encontrar uma função para , temos:
Temos então que:
Onde esse é igual a velocidade angular em , como o enunciado diz temos que em , logo .
Agora para até , temos:
Agora podemos encontrar uma função para , temos:
Temos então que:
Onde esse é igual a velocidade angular em que é onde a segunda parte do gráfico começa.
Utilizando a expressão que encontramos antes temos que , assim temos o seguinte
Com isso temos que:
Então sabendo disso temos que o nosso gráfico fica da seguinte forma:
Resposta
