Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 8.Exercícios e Problemas - Ex. 19
19. Um trem de brinquedo percorre um trilho horizontal com de diâmetro. O coeficiente de atrito de rolamento vale .
a. Quanto vale a aceleração angular do trem após ser liberado?
b. Quanto tempo decorre para que o trem pare depois de liberado com velocidade angular de ?
Passo 1
Opa! Aqui vamos nós de novo!
Olha só! Primeiramente vamos fazer o diagrama de corpo livre para o nosso carrinho a fim de entender o que está acontecendo...
A seguinte figura abaixo ilustra perfeitamente o que está acontecendo em nosso problema...
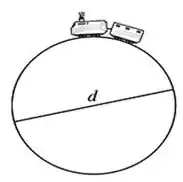
Com isso, chegamos ao seguinte diagrama de corpo livre:
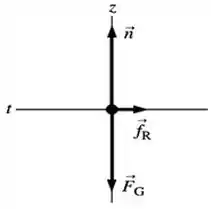
E quanto ao raio da trajetória circular do trem, ele vai valer...
Passo 2
a) Bom! Passada essa parte introdutória, vamos aplicar agora, o somatório das forças na vertical...
Obtemos então, que a normal é igual à força gravitacional. Desse modo, a próxima coisa a se fazer é obter a força de atrito agindo sobre o trem. Para isso, basta multiplicar o coeficiente de atrito pela normal.
Só que é justamente essa força de atrito, a responsável por desacelerar o trem, contando é claro que ele já esteja em movimento. Ela irá produzir a aceleração tangencial, que no caso vai ser contrária ao movimento do trem...
Mas já que o objetivo final é encontrar a aceleração angular... Bem! Para fazer isso, basta dividir a aceleração tangencial pelo raio da trajetória;
Passo 3
b) Olha só! A nossa velocidade angular inicial é...
Sendo assim, vamos usar a fórmula abaixo para encontrar o intervalo de tempo...
Isolando :
Onde substituindo os valores numéricos adequados...
Finalmente obtemos nossa resposta!
Resposta
a)
b)