Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Problemas - Ex. 42
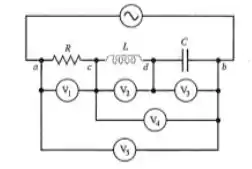
42 - Cinco voltímetros com impedância infinita, calibrados para medir o valor eficaz da tensão, são conectados conforme indicado na Figura 31.25. Seja , , e . Qual é a leitura de cada voltímetro quando
- ?
- ?
Passo 1
Bem, a corrente que passa no circuito é dado pela Lei de Ohm...
Onde é a tensão da fonte só que a gente tem que dividir por por que a tensão é de pico (então a gente divide para obter a RMS) e é a impedância geral do circuito dado por...
Como os ’s são reatâncias, podemos encontra-las usando ...
Como o módulo de é dado por Pitágoras, podemos encontrar...
Então quando e a tensão da fonte igual a ...
Então a tensão em cima de todos eles , é a medida da tensão em cima da fonte:
Já a tensão em cima do resistor...
Para as tensões e em cima dos indutores e capacitores...
Onde são as reatâncias calculadas com ...
Já a tensão em cima do capacitor...
Para a tensão , podemos calcular lembrando-se de que o módulo de tensão em cima dos elementos é a subtração do indutivo pelo capacitivo:
Passo 2
Agora precisamos fazer cálculos semelhantes só que dessa vez para e a tensão da fonte igual a ...
Então a tensão em cima de todos eles , é a medida da tensão em cima da fonte:
Já a tensão em cima do resistor...
Já a tensão em cima do capacitor...
Resposta
Ei, a resposta está no passo a passo :)