Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 32.Problemas - Ex. 42
42- Considere uma onda eletromagnética plana tal como a indicada na Figura , porém na qual os campos e também possuam componentes na direção do eixo (ao longo da direção de propagação da onda). Use a lei de Gauss para o campo magnético para mostrar que os componentes e devem ser ambos iguais a zero e que, portanto e são ambos transversais. (Sugestão: use uma superfície gaussiana como indicada na Figura . Das duas faces paralelas ao plano , escolha uma a esquerda da frente de onda e a outra a direita da frente de onda.)
Passo 1
A Lei de Gauss para o magnetismo nos diz que:
Desenhando a superfície gaussiana da figura e considerando que a onda magnética se propaga na direção de , nós teremos:
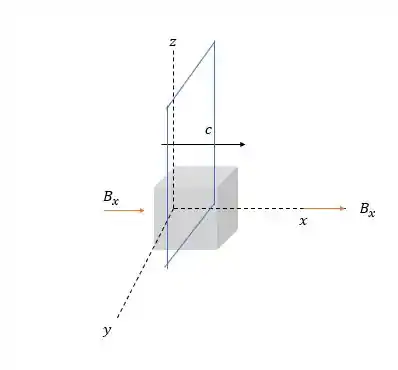
Fazendo a integral de linha nós teremos:
E como a área é área do cubo transversal (pelo frente da onda, representado pelas linhas azuis) a onda magnética então:
Passo 2
Agora aplicando a Lei de Gauss nós temos:
E considerando uma carga interna no meio da frente de onda nós teremos:
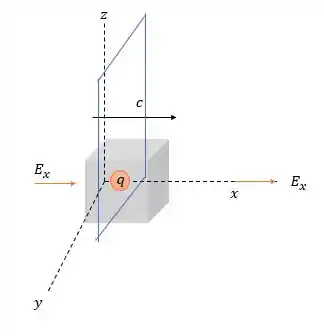
E como o campo elétrico continua na mesma direção (antes e depois de passar pela frente de onda) independente da carga interna então
E como temos uma área bem definida pela frente de onda então:
Então as ondas tem que ser transversais, pois somente dessa forma que teremos a propagação dessa onda.
Resposta
Ei, a resposta está no passo a passo :)