Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 32.3 - Ex. 7

Um capacitar de placas paralelas possui placas circulares de raio R = 30 m m e a distância entre as placas é 5,0 mm. Uma diferença de potencial senoidal com um valor máximo de 150 V e uma frequência de 60 Hz é aplicada às placas, ou seja, a tensão entre as placas é

V = 150 V s e n 2 π 60 H z t .

(a) Determine B m á x R , o valor máximo do campo magnético induzido a uma distância radial r = R. (b) Plote B m á x r para 0 < r < 10 c m .

Passo 1

E aí! tudo certinho? 😉

Nesse problema temos um capacitar de placas paralelas que possui placas circulares de raio R = 30 m m e a distância entre as placas é 5,0 mm. Uma diferença de potencial senoidal com um valor máximo de 150 V e uma frequência de 60 Hz é aplicada às placas, ou seja, a tensão entre as placas é

V = 150 V s e n 2 π 60 H z t .

A partir daí queremos determinar B m á x R , o valor máximo do campo magnético induzido a uma distância radial r = R e queremos plotar B m á x r para 0 < r < 10 c m .

Parece complicado? 😬

Veja só! 😉

Passo 2

Bem, primeiramente, vamos utilizar a resposta do exemplo “Campo magnético induzido por um campo elétrico variável”:

B = μ 0 ε 0 r 2 d d V d t

Como, V = V m a x s e n ω t , temos:

d V d t = V m a x ω c o s ω t

Portanto:

B = μ 0 ε 0 r 2 d V m a x ω c o s ω t

Como, temos que achar o valor máximo do campo, temos que o valor máximo do cosseno é 1, assim:

B m a x = μ 0 ε 0 R 2 d V m a x ω

Substituindo os valores do enunciado, temos

B m a x = 4 π × 10 - 7 8,85 × 10 - 12 30 × 10 - 3 2 5,0 × 10 - 3 150 2 π 60

B m a x = 1,88 × 10 - 1 2 T

Tranquilo até aqui? 😎

Passo 3

(b) Primeiramente, temos que perceber que o resultado do item anterior serve apenas para a região interna a placa. Agora, para a região externa, vamos utilizar o item (b) do exemplo “Campo magnético induzido por um campo elétrico variável”:

B = μ 0 ε 0 R 2 2 r d d V d t = μ 0 ε 0 R 2 2 r d V m a x ω c o s ω t

B m a x = μ 0 ε 0 R 2 2 r d V m a x ω

Substituindo os valores:

B m a x = 1 r 4 π × 10 - 7 8,85 × 10 - 12 30 × 10 - 3 2 2 5,0 × 10 - 3 150 2 π 60

B m a x r = 1,77 × 10 - 23 1 r

Plotando:

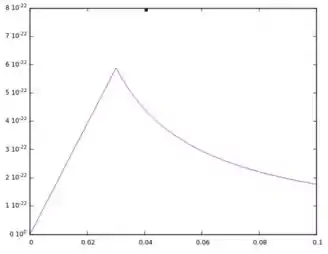
E aí! o que achou? Responde Aí! 😊

Resposta

(a) B m a x = 1,88 × 10 - 12 T

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

6 - Uma onda eletromagnética com comprimento de onda igual a 435n m se desloca no vácuo no sentido - z . O campo elétrico é paralelo ao eixo O x e possui amplitude de 2,70 ×10 - 3 V / m . Qual é o val
12- A amplitude do campo elétrico nas vizinhanças de uma certa estação de rádio é igual a 3.85 × 10 - 3V / m . Qual é a amplitude de B → ? Como o valor obtido se compara ao módulo do campo magnético d
14- Uma onda eletromagnética com frequência de 6.50H z se desloca em um material magnético isolante que possui constante dielétrica de 3.64 e permeabilidade relativa de 5.18 nessa frequência. O campo
13- Uma onda eletromagnética com frequência 5.70 × 10 14H z se propaga com uma velocidade de 2.17 × 10 8m / s em um dado pedaço de vidro. Determine ( a ) o comprimento de onda da onda no vidro; ( b )
11- Uma certa estação de rádio emite ondas com frequência de 830k H z . Para uma dada distância do transmissor, a amplitude do campo magnético da onda eletromagnética é igual a 4.82 × 10 - 11T . Calcu