Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 32.3 - Ex. 10

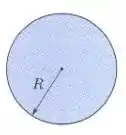
Fluxo el��trico não uniforme. A Fig. 32-30 mostra uma região circular de raio R = 3,00 c m na qual um fluxo elétrico aponta para fora do papel. O fluxo elétrico envolvido por uma circunferência concêntrica de raio r é dado por Φ E e n v = 0,600 V · m / s r / R t ,

onde r ⩽ R e t está em segundos. Determine o módulo do campo magnético induzido a uma distância radial (a) de 2,00 cm; (b) de 5,00 cm.

Passo 1

Fala aí, galerinha! 😉

Nesse problema temos uma região circular de raio R = 3,00 c m na qual um fluxo elétrico aponta para fora do papel. O fluxo elétrico envolvido por uma circunferência concêntrica de raio r é dado por

Φ E e n v = 0,600 V · m / s r / R t

onde r ⩽ R e t está em segundos.

A partir daí temos que determinar o módulo do campo magnético induzido a uma distância radial de 2,00 cm e de 5,00 cm.

Parece complicado? 😁

Para resolver esse problema, para a parte de dentro da região circular, podemos começar aplicando a seguinte equação:

∫ B d s = μ 0 ε 0 d Φ d t

Veja só! 😬

Passo 2

Se

∫ B d s =   B 2 π r

E como o fluxo é uniforme...

d Φ d t = 0,600 V · m / s r / R

Temos

B 2 π r = μ 0 ε 0 0,600 V · m / s r / R

B = μ 0 ε 0 2 π R 0,600 V · m / s

O valor de r não é usado na equação. Portanto o campo dentro é:

B = 4 π × 10 - 7 8,85 × 10 - 12 2 π 0,0300 0,600 V · m / s

B = 3,54 × 10 - 17 T

Tranquilo até aqui? 👀

Passo 3

(b) Quando saímos da região circular, temos que pegar o valor máximo do fluxo, portanto:

B 2 π r = μ 0 ε 0 0,60

B = μ 0 ε 0 2 π r 0,60

Substituindo os valores...

B = 4 π × 10 - 7 8,85 × 10 - 12 2 π 0,0500 0,60

B = 2,13 × 10 - 17 T

E então? Entendeu tudo? Responde Aí! 😐

Resposta

(a) B = 3,54 × 10 - 17 T

(b) B = 2,13 × 10 - 17 T

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8 - O campo elétrico de uma onda eletromagnética senoidal obedece à equação E=–( 375V / m )s e n [ ( 5,97 ⋅10 15r a d / s ) t+( 1,99 ⋅ 10 7r a d / m ) x ] . Quais são a frequência, o comprimento de on
10 - Uma onda eletromagnética possui um campo magnético dado por B → ( x ,t )=( 8,25 × 10 - 9T )j ^s e n[ ( 1,38 ×10 4r a d / m ) x+ ω t ] .Em que direção e sentido a onda eletromagnética está se prop
7 - Uma onda eletromagnética senoidal com frequência igual a 6 , 10 ×10 14H z se desloca no vácuo no sentido + z . O campo magnético B é paralelo ao eixo O y e possui amplitude de 5,80 ×10 - 4 T . Esc
9 - Uma onda eletromagnética possui um campo elétrico dado por E → y ,t = -( 3,10x10 5V / m )k ^s e n[ k y–( 12,65x10 12r a d / s ) t ] .Em que direção e sentido a onda eletromagnética esta se propaga
5 - Uma onda eletromagnética senoidal com um campo magnético de amplitude 1,25µ T µ e um comprimento de onda de 432n m se desloca no sentido + x através do vácuo.Qual é a frequência dessa onda? Qual é