Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Problemas - Ex. 49

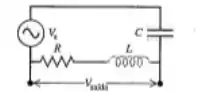
49 - Um filtro passa-altos. Uma aplicação do circuito R-L-C em série consiste no uso de um filtro passa-altos ou de um filtro passa-baixos, que filtram, respectivamente, os componentes de baixa frequência ou os componentes de altas frequências de um determinado sinal. Um filtro passa-altos é indicado na Figura 31.26, em que a tensão de saída é tomada através da combinação L-R. (A combinação L-R representa uma bobina de indução que também possui uma resistência, pois seu enrolamento é um fio com um comprimento muito grande.) Deduza uma expressão para V s a í d a / V s , a razão entre a amplitude da tensão na saída e a amplitude da tensão da fonte, em função da frequência angular ω da fonte. Mostre que, quando ω é pequeno, essa razão é proporcional a ω e, portanto, é pequena, e mostre que ela tende a 1 no limite de frequências elevadas.

Passo 1

Antes de qualquer coisa, perceba que podemos encontrar a corrente total que o sistema está exigindo da fonte pela fórmula...

I = V s R 2 + ω L - 1 ω C 2

A tensão de saída então é dada pela impedância vezes a corrente:

V s a í d a = Z s a í d a I  

Poxa, a impedância de saída é formada por um resistor e por um indutor somente em série, então a impedância de saída pode ser dada assim:

Z s a í d a = R 2 + ω 2 L 2

Logo, podemos então falar que a tensão de saída é...

V s a í d a = Z s a í d a I       →

V s a í d a = R 2 + ω 2 L 2 ⋅ V s R 2 + ω L - 1 ω C 2   →

Passando o V s pro outro lado e colocando as raízes dentro de uma só, a gente obtém o que a razão que queríamos no problema, veja:

V s a í d a V s = R 2 + ω 2 L 2 R 2 + ω L - 1 ω C 2

Passo 2

Então agora vejamos o que acontece com a relação à medida que ω vai diminuído a 0 :

V s a í d a V s = R 2 + ω 2 L 2 R 2 + ω L - 1 ω C 2       →

Perceba que no numerador vai sobrar só R 2 . Enquanto que no denominado...

V s a í d a V s = R 2 R 2 + - 1 ω C 2     →

Agora perceba que à medida que ômega vai a 0 , 1 ω C vai para o infinito, tornando R 2 cada vez mais indiferente, então a gente pode elimina-lo do denominador...

V s a í d a V s = R 2 1 ω 2 C 2 =

ω R C

Passo 3

Vamos fazer a mesma análise de limite só que agora vendo o que acontece considerando ω → ∞ :

V s a í d a V s = R 2 + ω 2 L 2 R 2 + ω L - 1 ω C 2       →

Bem quando ω vaia para ∞ a fração vai a 0 :

V s a í d a V s = R 2 + ω 2 L 2 R 2 + ω L 2       →

V s a í d a V s = R 2 + ω 2 L 2 R 2 + ω 2 L 2       →

V s a í d a V s = 1 = 1

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

45 - Um circuito em série possui uma impedância de 60 Ω e um fator de potência igual a 0,720 para 50,0 H z . A tensão da fonte está atrasada em relação à corrente. Que elemento de circuito, um indutor
40 - A Figura 31.12a representa um corte de um alto-falante, indicando os circuitos usados no sistema. Um ramo é constituído por um capacitor C e por um resistor R em série (o tweeter). Esse ramo está
48 - Para uma frequência ω 1 , a reatância de um certo capacitor é igual à reatância de um certo indutor. Se a frequência variar para ω 2 = 2 ω 1 , qual deverá ser a razão entre a reatância do indutor
56 - Um resistor de 400Ω e um capacitor de 6,0p F são conectados em paralelo com um gerador CA que fornece uma tensão eficaz de 220V para uma frequência angular de 360r a d / s . Use os resultados do