Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 31.Problemas - Ex. 43

43 - Uma corrente senoidal é dada por i = I cos ⁡ ω t . A corrente obtida por um retificador de onda completa é indicada na Figura 31.3b.

  1. Sejam t 1 e t 2 os menores tempos positivos para os quais a corrente retificada é igual a zero. Expresse t 1 e t 2 em termos de ω .
  2. Calcule a área embaixo da curva retificada de i contra t entre t 1 e t 2 calculando a integral ∫ t 1 t 2 i   d t . Como d q = i   d t , essa área é igual à carga que flui entre os instantes t 1 e t 2 .
  3. Iguale o resultado do item (b) com I r m t 2 - t 1 = A e calcule I r m em termos da amplitude da corrente I . Compare sua resposta à Equação (31.3).

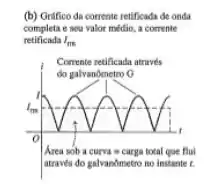
Passo 1

L e t r a   A :

Pois bem, os dois menores valores t 1 e t 2 o qual a corrente é 0 acontece nesses dois primeiros pontos em vermelho aqui destacado:

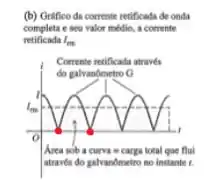
Para encontrar esses pontos, sabemos que ele vem zerando o cosseno:

i = I cos ⁡ ω t = 0     →

cos ⁡ ω t = 0

Ora, o cosseno é 0 quando ω t = π 2 , e ω t = 3 π 2 e assim por diante. Esses são os dois menores valores positivos para os quais o cosseno se torna zero. Então...

t 1 = π 2 ω         e               t 2 = 3 π 2 ω

Passo 2

L e t r a   B :

∫ t 1 t 2 i   d t =

∫ π 2 ω 3 π 2 ω I cos ⁡ ω t   d t

Integrando o cosseno lembrando-se de que I é constante...

∫ π 2 ω 3 π 2 ω I cos ⁡ ω t   d t = I sin ⁡ ω t ω π 2 ω 3 π 2 ω =

I sin ⁡ ω 3 π 2 ω ω - sin ⁡ ω π 2 ω ω =

I sin ⁡ 3 π 2 ω - sin ⁡ π 2 ω =

Lembrando-se do seno de π / 2 e 3 π / 2 ...

I - 1 ω - 1 ω = - 2 I ω

Passo 3

L e t r a   C :

I r m s t 2 - t 1 = A

Onde A é o módulo da área que calculamos...

A = - 2 I ω =

2 I ω

Então...

I r m s t 2 - t 1 = 2 I ω   →

I r m s π 2 ω - 3 π 2 ω = 2 I ω     →

I r m s = 2 I π

E essa equação é exatamente a mesma coisa que a equação pedida.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

68 - Uma resistência R , uma capacitância C e uma indutância L são ligadas em série a uma fonte com amplitude de voltagem V e frequência angular variável ω . Sendo ω = ω 0 a frequência angular da ress
72. No circuito indicado na Figura 30.30 , nem a bateria nem os indutores possuem resistência interna significativa, os capacitores não possuem carga inicial e a chave S está na posição 1 há um longo
68. No circuito indicado na Figura 30.27 , ε = 60,0V , R 1 = 40,0Ω , R 2 = 25Ω e L = 0,300H . ( a ) A chave S está fechada. Em um instante t posterior, a corrente no indutor está crescendo com uma tax
65. No circuito indicado na Figura 30.25 , a chave S é fechada no instante t = 0 . ( a ) Determine a leitura de cada instrumento logo após a chave S ser fechada. ( b ) Qual é a leitura após a chave S
71. No circuito indicado na Figura 30.29 , a chave está aberta há muito tempo, quando é subitamente fechada. Nem a bateria nem os indutores possuem resistência interna significativa. Revise os resulta