Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 36.Problemas - Ex. 58
58. A intensidade da luz na figura da difração de Fraunhofer de uma fenda única é
onde
Mostre que a equação que fornece os valores de correspondentes aos máximos é dada por . Determine os três menores valores positivos de que são soluções dessa equação. (Sugestão: você poderá usar o método das tentativas. Estime um valor inicial para e ajuste sua tentativa de modo a tornar o valor de o mais próximo possível de . Uma solução gráfica da equação é muito útil para fazer a estimativa do valor inicial.)
Passo 1
Para mostrar o que é pedido em vamos usar nossos conhecimentos de cálculo e lembrar que para uma função ter máximo a derivada dela tem que ser zero.
Então vamos derivar a intensidade em relação a e ir mexendo na expressão para encontrarmos o que o item quer.
Para o item vamos usar a expressão que queremos chegar em , temos o seguinte:
Podemos definir uma função e fazer o gráfico dessa função e ver os valores de que zeram essa função, pois:
Passo 2
Vamos mostrar o que é pedido em , temos o seguinte:
Fazendo , temos:
E temos que:
Manipulando essa equação um pouco.
Dividindo os dois lados por , temos que:
Passo 3
Agora vamos fazer o gráfico da função que comentei no passo com vocês e encontrar valores de que zerem essa função. Temos:
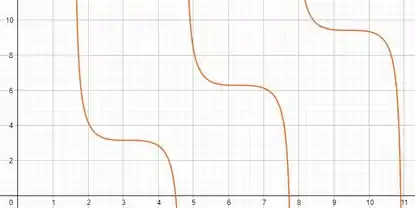
O item quer os três menores valores positivos de .
Olhando o gráfico dá para ver mais ou menos que a função zera em , e em
Se testarmos esses valores na nossa função vemos que ela bem dizer zera.