Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 30.Problemas - Ex. 60
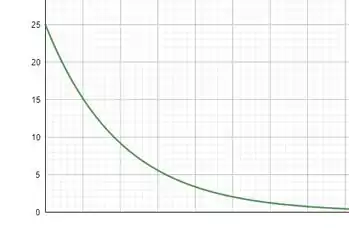
60. Ao estudar uma bobina de indutância e resistência internas desconhecidas, você a conecta em série a uma bateria de e a um resistor de . A seguir, você conecta um osciloscópio a um desses elementos de circuito e o utiliza para medir a voltagem que passa pelo elemento de circuito em função do tempo. O resultado é indicado na figura . A qual elemento de circuito (bobina ou resistor) o osciloscópio está conectado? Como você sabe? Determine a indutância e a resistência da bobina. Cuidadosamente, faça um desenho quantitativo da voltagem contra o tempo que você observaria, se conectasse o osciloscópio ao outro elemento de circuito (resistor ou bobina).
Passo 1
Bem, para se obter o resultado que é mostrado na figura o osciloscópio está colocado no resistor. Já que a voltagem no resistor se comporta com a corrente que varia no tempo. A voltagem no resistor é dada por:
E do circuito se comporta da seguinte maneira:
No gráfico podemos ver que como , para que não haja queda de tensão no indutor temos que sua resistência interna deve ser zero.
Agora vamos juntar as duas equações acima e obtemos que:
Onde vamos chamar , assim:
Tendo isso vamos considerar que passa um intervalo de tempo e ver que valor de voltagem no resistor, tendo isso podemos olhar no gráfico e ver qual valor de isso representa, tendo esse valor podemos achar a indutância, já que:
Passo 2
Vamos então encontrar o valor da indutância, temos:
Fazendo , temos:
Sabendo que , temos:
Se olhamos no gráfico temos que essa voltagem acontece mais ou menos em
Então temos que:
Onde , logo:
Passo 3
Bem o gráfico mostrado no enunciado é com o osciloscópio conectado ao resistor, então agora para o item, ele é conectado na bobina, que no caso vai ter a voltagem descrendo de forma proporcional ao crescimento da voltagem no resistor, então o gráfico fica da seguinte maneira:
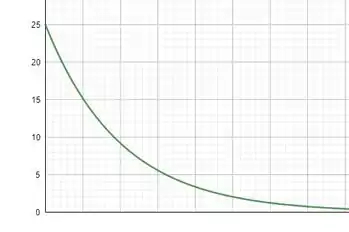
Resposta
O osciloscópio está conectado ao resistor.
