Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.2 - Ex. 7

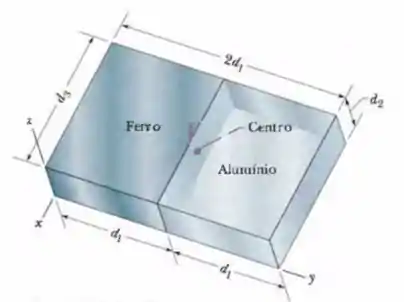
A Fig. 9-36 mostra uma placa composta de dimensões d 1 = 11,0   c m , d 2 = 2,80   c m e d 3 = 13,0   c m . Metade da placa é feita de alumínio (massa especifica = 2,70   g / c m 3 ) e a outra metade de ferro (massa especifica = 7,85   g / c m 3 ). Determine (a) a coordenada x , (b) a coordenada y e (c) a coordenada z do centro de massa da placa.

Passo 1

Oi, galerinha! Tudo bom? Aqui nós temos a junção de uma placa de metálica de alumínio e uma de ferro, que possuem densidades diferentes. Deste modo, para calcular a coordenada de cada eixo do centro de massa podemos usar as seguintes relações:

x c m = m 1 x 1 + m 2 x 2 m 1 + m 2

y c m = m 1 y 1 + m 2 y 2 m 1 + m 2

z c m = m 1 z 1 + m 2 z 2 m 1 + m 2

Porém, devemos perceber que a distribuição de massa nas coordenadas x e z apresentam simetria, portanto, não precisamos usar estas relações para essas coordenadas.

Passo 2

  1. Para a coordenada x , como há simetria:

    2. x c m = - d 3 2 = - 13 2 = - 6,5   c m

    O sinal de negativo foi representado para estar de acordo com o eixo de referência adotado.

    Passo 3

  2. Para a coordenada y , usaremos a relação dada no passo inicial:

    3. y c m = m 1 y 1 + m 2 y 2 m 1 + m 2

    Lembrando que:

    m = ρ V

    Onde, ρ é a densidade do material e V é o volume. Assim:

    y c m = ρ 1 V 1 y 1 + ρ 2 V 2 y 2 ρ 1 V 1 + ρ 2 V 2

    Devemos perceber que o volume das duas placas são iguais e que a posição do centro de massa de cada uma está no centro da placa de cada uma. Assim:

    y c m = ρ 1 d 1 2 + ρ 2 d 1 + d 1 2 ρ 1 + ρ 2

    Substituindo os valores:

    y c m = 7,85 × 11 2 + 2,7 × 11 + 11 2 7,85 + 2,7

    y c m = 8,32   c m

    Passo 4

  3. Para a coordenada z , usaremos a simetria novamente:

z c m = d 2 2 = 2,8 2

z c m = 1,4   c m

Resposta

  1. x c m = - 6,5   c m ;
  2. y c m = 8,32   c m ;
  3. z c m = 1,4   c m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três massas pontuais de 2,0k g cada estão localizadas sobre o eixo x . Uma está sobre a origem, outra em x = 0,20m e outra em x = 0,50m . Encontre o centro de massa do sistema.
Em uma escavação arqueológica de fim de semana, você descobre um antigo martelo que consiste de uma pedra simétrica de 8,0k g presa na ponta de um pedaço de madeira uniforme de 2,5k g . Você mede as d
Três bolas, A , B e C , com massas 3,0k g , 1,0k g e 1,0k g , respectivamente, estão conectadas por hastes sem massa, como mostrado na figura. Quais são as coordenadas do centro de massa do sistema.
Por simetria, localize o centro de massa de uma folha uniforme em forma de triângulo equilátero com lados de comprimento a . O triângulo tem um vértice no eixo y e os outros em ( - a 2 , 0 ) e ( + a 2
Duas hastes finas, uniformes e idênticas, cada uma de comprimento L , estão coladas nas extremidades uma da outra de forma que o ângulo na junção é de 90 ° . Determine a localização do centro de massa