Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 9.2 - Ex. 4
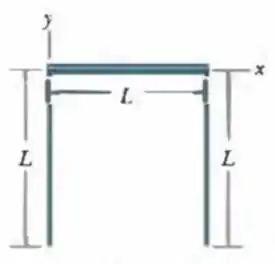
Na Fig. 9-37, três barras finas e uniformes, de comprimento , formam um invertido. Cada barra vertical tem uma massa de ; a barra horizontal tem massa de . Quais são (a) a coordenada e (b) a coordenada do centro de massa do sistema?
Passo 1
Oi, galerinha! Tudo bom? Para calcular a coordenada de cada eixo do centro de massa podemos usar as seguintes relações:
Onde, é a massa de cada partícula, é a posição do centro de massa no eixo e é a posição do centro de massa no eixo .
Para quem não, o centro de massa de uma barra homogênea se encontra bem no centro dela!
Agora vamos calcular!
Calculando o somatório das massas que se repetem em todas as equações:
Passo 2
Para não termos que fazer conta por fazer, devemos primeiro buscar uma simetria no problema. Neste caso, percebemos que no eixo há uma simetria na distribuição de massa. Assim, para determinar a posição de vamos usar apenas o argumento da simetria ao invés de calcular usando a relação dada no passo anterior. Portanto:
Passo 3
Já para a coordenada não conseguimos perceber nenhuma simetria e, portanto, devemos usar a relação dada no passo inicial. Para tanto, vamos perceber que o centro de massa de cada barra em relação ao eixo é:
Assim:
Resposta
- ;
- .