Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 36.Problemas - Ex. 61
61. Diagrama de fasores para oito fendas. Uma figura de interferência é formada por oito fendas estreitas igualmente espaçadas. A Figura mostra diagramas de fasores para os casos em que a diferença de fase entre duas ondas provenientes de fendas adjacentes é dada por e . Cada um desses casos fornece um mínimo. A legenda da Figura também afirma que podem ocorrer mínimos para e . Desenhe um diagrama de fasores para cada um desses casos e explique por que cada diagrama prova de fato a existência de um mínimo. (Neta: talvez você ache útil usar uma cor diferente para cada fenda!) Em cada um dos quatro casos e , em quais pares de fendas ocorre interferência destrutiva total?
Passo 1
Então galera, esse exercício em sua maior parte é desenhar o diagrama de fasores e vamos tomar como exemplo a figura .
Uma observação é que como temos oito fendas teremos oito fasores.
Explicando de forma simples teremos que desenhar cada fasor com a inclinação referente a cada fase que estamos analisando onde vamos ligar o final de um com o início do outro, na figura do livro você pode notar isso.
Passo 2
Vamos lá então.
Primeiro para que é a mesma coisa que . Temos:
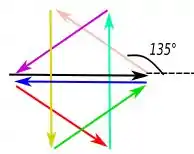
Nós temos mínimo porque a soma de todos os fasores das oito fendas soma zero. Eles formam um caminho fechado.
Passo 3
Agora para que é a mesma coisa que ou . Temos:
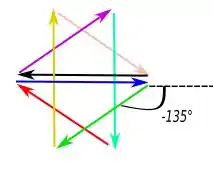
Nós temos mínimo porque a soma de todos os fasores das oito fendas soma zero. Eles formam um caminho fechado.
Passo 4
Agora para que é a mesma coisa que ou . Temos:
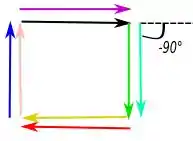
Nós temos mínimo porque a soma de todos os fasores das oito fendas soma zero. Eles formam um caminho fechado.
Passo 5
Agora para que é a mesma coisa que ou . Temos:
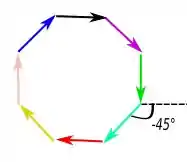
Nós temos mínimo porque a soma de todos os fasores das oito fendas soma zero. Eles formam
um caminho fechado.
Passo 6
Então vamos analisar o que é pedido em .
Para que tenhamos interferência totalmente destrutiva temos que ter uma diferença de fase ou seja números ímpares multiplicados por .
Dos diagramas de fasores vemos que cada fenda contribui com uma diferença de fase .
Para o caso em que , vemos que a cada fendas temos , logo interferência totalmente destrutiva.
Para o caso em que , vemos que a cada fendas temos , logo interferência totalmente destrutiva.
Para o caso em que , vemos que a cada fendas temos , logo interferência totalmente destrutiva.
Para o caso em que , vemos que a cada fendas temos , logo interferência totalmente destrutiva.
Resposta
Para :
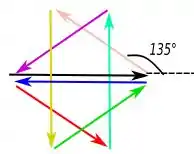
Para :
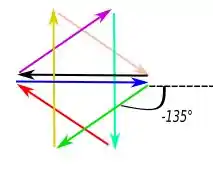
Para :
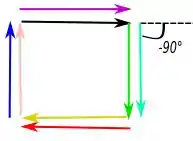
Para :
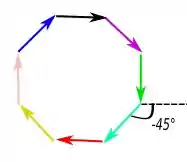
Para , , temos interferência totalmente destrutiva a cada fendas e para temos interferência totalmente destrutiva a cada fendas.