Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 27.7 - Ex. 28

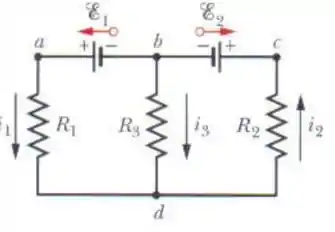
Na Fig. 27-9, determine a diferença de potencial V d - V c entre os pontos d e c se ε 1 = 4,0 V , ε 2 = 1,0 V , R 1 = R 2 = 10   Ω , R 3 = 5,0   Ω e a fonte é ideal.

Passo 1

Olá, meu nobre amigo. Yuri aqui e eu estarei te ajudando a resolver essa atividade. Aqui iremos encontrar a diferença de potencial entre dois pontos do circuito. Iremos utilizar a Lei das malhas para isso.

Passo 2

Separando cada parte do circuito, para a malha esquerda temos:

ε 1 – i 1 R 1 + i 3 R 3 = 0

Agora, para a parte da direita:

- ε 2 – i 3 R 3 - i 2 R 2 = 0

Usando o fato que

i 3 = i 2 - i 1

Podemos reescrever as duas equações:

i 1 R 3 + R 1 - ε 1 - i 2 R 3 = 0

i 2 R 3 + R 2 + ε 2 - i 1 R 3 = 0

Isolando as correntes 2 na equação de baixo:

i 2 = i 1 R 3 - ε 2 R 3 + R 2

Dessa forma, podemos substituir a corrente 2 na equação da corrente 1:

i 1 R 1 R 2 + R 3 R 2 + R 1 R 3 + ε 1 R 3 + R 2 + ε 2 R 3 = 0

i 1 = ε 1 R 2 + R 3 - ε 2 R 3 R 1 R 2 + R 3 R 2 + R 1 R 3

Fazendo a mesma coisa para a corrente 2:

i 2 = ε 1 R 3 - ε 2 R 1 + R 3 R 1 R 2 + R 3 R 2 + R 1 R 3

Passo 3

Agora, podemos calcular as correntes:

i 1 = 4,0 10 + 5,0 - 1,0 5,0 10 10 + 5,0 10 + 10 5,0 = 0,275 A

i 2 = 4,0 5,0 - 1,0 10 + 5,0 10 10 + 5,0 10 + 10 5,0 = 0,025 A

E a para a corrente i 3 :

i 3 = 0,025 – 0,275 = - 0,250 A

Passo 4

Dado que o potencial ( V c ) é o mesmo que o potencial no terminal superior do resistor ( R 2 ) (assumindo que o potencial não muda, uma vez que a resistência do fio é negligenciável) e o potencial ( V d ) é o mesmo que o potencial no terminal inferior do resistor ( R 2 ) , isso significa que a diferença de potencial ( Δ V c d ) é a mesma que a queda de voltagem no resistor ( R 2 ) , ou seja,

Δ V c d = I 2 ⋅ R 2

= 0.025 ∙ 10

= 0.25   V

Resposta

Δ V d c = 0,25 V

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

27.37. Na Fig. 27-48 as resistências R 1 = 1,0Ω e R 2 = 2,0Ω e as forças eletromotrizes das fontes ideias são ξ 1 = 2,0V , ξ 2 = 4,0V e ξ 3 = 4,0V . Determine (a) o valor absoluto e (b) o sentido (par
a) Calcule a resistência equivalente (em termos de R, a resistência de cada um dos resistores) entre os pontos a e b para a escada infinita de resistores mostrada na Figura 25-80, considerando que os
Duas baterias com fems ε 1 e ε 2 e resistências internas r 1 e r 2 , estão conectadas em paralelo. Prove que, se um resistor de resistência R é conectado em paralelo ecom a combinação, a resistência ó
Na Figura 25-50, os valores das resistências estão relacionados como segue R 2 = R 3 = 2 R 1 . Se a potência P é fornecida a R 1 , qual é a potência fornecida a R 2 e a R 3 ?
Um comprimento de arame tem uma resistência de 120Ω . O arame é cortado em pedaços que têm o mesmo comprimento, e então os arames são conectados em paralelo. A resistência do arranjo paralelo é de 1,8