Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 7.Problemas - Ex. 80
. Um próton de massa move-se em uma dimensão. A função da energia potencial é dada por , onde e são constantes positivas. O próton é libertado a partir do repouso no ponto . Mostre que pode ser escrita do seguinte modo
Faça um gráfico de . Calcule e localize o ponto no gráfico. Calcule , a velocidade do próton em função da posição. Faça um gráfico de e forneça uma descrição qualitativa do movimento. Para qual valor de a velocidade do próton é máxima? Qual é o valor dessa velocidade máxima? Qual é a força que atua sobre o próton no ponto calculado no item ? Em vez de considerar o ponto inicial anterior, suponha que o próton seja liberado no ponto . Localize o ponto no gráfico de . Calcule e forneça uma descrição qualitativa do movimento. Para cada ponto em que o próton
é liberado e , determine os valores máximo e mínimo de atingidos durante o movimento.
Passo 1
Vem comigo que a gente se livra dessa questão.
Duas coisas importantes que vamos precisar nessa questão são a conservação de energia mecânica, dada por:
E a relação entre energia potencial e uma força conservativa, dada por, na direção :
A partir disso podemos encontrar o que cada item pede. Vamos fazer um de cada vez para não nos embolarmos.
Passo 2
Vamos começar com o item .
Ele quer que a gente chegue em uma outra forma de escrever a energia potencial, dada no enunciado.
O que temos inicialmente é o seguinte:
E ele nos dá também que:
Vamos isolar o nessa segunda equação, assim temos:
Substituindo na primeira, temos:
Se isolarmos , ficamos com:
Prontinho, chegamos aonde ele queria.
Agora o gráfico de é da seguinte forma:
Passo 3
Agora o gráfico de é da seguinte forma:
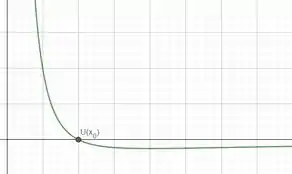
Ele que também saber quanto vale , assim:
Então temos que:
Como mostra o gráfico.
Passo 4
Agora vamos para o item .
Para encontrar uma expressão para vamos usar a conservação de energia, temos que:
O gráfico dessa função é da seguinte forma:
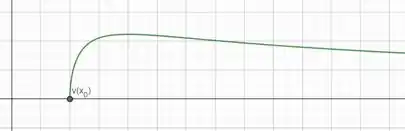
Olhando o gráfico vemos que o próton ganha velocidade a partir do ponto até atingir sua velocidade máxima depois tem uma diminuição, mas ele nunca para.
Passo 5
Agora para o item .
Para achar a posição onde temos a velocidade máxima e o valor dessa velocidade, temos que lembrar que pela conservação de energia a energia cinética vai ser máxima quando a energia potencial for mínima.
Então temos que achar o valor de que faz com que seja mínimo, para isso vamos usar o cálculo ao nosso favor, sabemos que isso irá acontecer quando:
Então:
Então temos que:
Essa é a posição onde temos a velocidade máxima do próton.
Passo 6
Agora vamos encontrar essa velocidade máxima, temos que:
Então temos que a velocidade máxima é dada por:
Passo 7
Agora vamos para o item .
Agora ele quer a força sobre próton na posição onde temos a velocidade máxima. Sabemos que:
Só que a gente viu no item anterior que a velocidade máxima acontece quando
Então temos que nesse ponto.
Passo 8
Vem comigo para o item .
Para localizar o ponto basta usarmos a função para , assim:
Então temos que:
Agora vamos calcular a , só que agora temos uma energia potencial inicial, assim:
Agora como a função da energia potencial não mudou a velocidade máxima ainda ocorre em e a partícula fica confinada entre e um outro valor mínimo.
Passo 9
Agora vamos para o último, item .
Esse item quer saber os valores de máximo e mínimo do fóton quando ele é liberado de e .
Quando o fóton é liberado , temos que a energia potencial é dada por:
Onde só tem um mínimo em , então ela segue até o infinito e não tem nenhuma distância máxima.
Agora quando a partícula é liberada de , temos que:
Então temos que a energia é zero em e em , então o próton fica confinado nesse intervalo.
Resposta
Demonstrado acima.
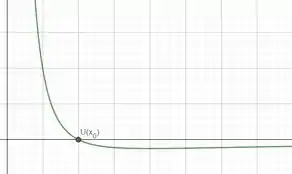
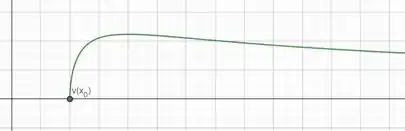
De até o infinito.
De até .