Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 23.Exercícios - Ex. 79
O potencial elétrico em uma região que está dentro de de origem de um sistema de coordenadas retangulares é dado por , em que , , , , , e são constantes. As unidades de , , e são tais que, se , e estão em metros, então está em volts. Você mede e cada componente do campo elétrico em quatro pontos e obtém os seguintes resultados:
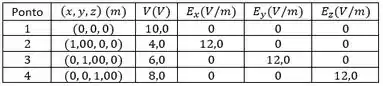
Use os dados na tabela para calcular , , , , , e . Determine e o módulo de nos pontos , e .
Passo 1
Vem comigo que essa a gente resolve juntos!
Para encontrar as constantes pedidas em vamos usar duas coisas, a primeira e a função de que o enunciado nos deu junto com os valores da tabela e segundo as seguintes equações:
Junto com os valores de e referentes aos pontos da tabela.
Para encontrar o e o módulo de nos pontos que o item pede, vamos usar as constantes que encontramos na função de e as mesmas equações que relacionam o potencial com o campo.
Tendo o valor de cada componente do campo, basta fazermos o seguinte:
Vamos as contas então!
Passo 2
Começando com o item .
Primeiro vamos avaliar a função de em cada ponto da tabela.
:
:
:
:
Agora temos que encontrar os valores de .
Passo 3
Vamos usar as equações que vimos no passo . Temos que:
Usando o que achamos para e as informações do ponto , temos:
Agora temos:
Usando o que achamos para e as informações do ponto , temos:
E por último:
Usando o que achamos para e as informações do ponto , temos:
Juntando tudo, temos que:
Passo 4
Agora vamos para o item .
A nossa função de , ficou da seguinte forma:
Agora vamos analisar essa função nos pontos que o enunciado pediu.
Primeiro :
Usando as equações para as componentes de , temos:
Logo temos que:
Passo 5
Segundo :
Usando as equações para as componentes de , temos:
Logo temos que:
Passo 6
E por último :
Usando as equações para as componentes de , temos:
Logo temos que:
Finalmente conseguimos terminar essa questão!
Resposta
Para :
Para :
Para :