Uma única força conservativa atua sobre uma pequena esfera de massa enquanto ela se move ao longo do eixo . Você solta a esfera do repouso em . À medida que ela se move, você mede sua velocidade em função da posição. Você usa os dados de velocidade para calcular a energia cinética ; a Figura mostra seus dados. Considere
que seja a função da energia potencial para . é simétrico em relação a ? [Se for, então .] Se você definir em , qual é o valor de em ? Desenhe o gráfico de . Em que valores de (se houver algum) ? Para que intervalo de valores de entre e é positivo? E negativo? Se você soltar a esfera do repouso em , qual é o maior valor de que ela alcança durante seu movimento? E qual o maior valor de energia cinética que ela tem durante seu movimento?
Passo 1
Vem comigo que a gente se livra dessa questão.
Duas coisas importantes que vamos precisar nessa questão são a conservação de energia mecânica, dada por:
E a relação entre energia potencial e uma força conservativa, dada por, na direção :
A partir disso e do gráfico fornecido pelo enunciado a gente vai resolver os itens dessa questão. Vamos fazer um de cada vez para não nos embolarmos.
Passo 2
Vamos começar com i tem .
Ele quer saber se a função é simétrica em relação a . Sabemos que a soma da energia cinética com a energia potencial deve ser constante pela conservação de energia.
Olhando pro gráfico de vemos que ele é simétrico, e que se dois pontos têm a mesma energia cinética eles vão ter a mesma energia potencial por conta da conservação de energia.
Então se a energia cinética é simétrica, a energia potencial também será simétrica.
Passo 3
Agora vamos para o item .
Queremos encontrar o valor de em levando em conta que em temos .
A gente tem o valor de em , do gráfico de , temos que em a energia cinética é , então pela conservação de energia temos que:
Logo temos que a energia total é .
Agora que conhecemos a energia total do sistema a gente pode usar isso para achar em , usando também a conservação de energia. Pelo gráfico de , a gente consegue ver que nesse ponto , logo:
Passo 4
Agora vamos para o item .
Agora ele quer o gráfico de , para montar esse gráfico basta usarmos a conservação de energia, já sabemos que:
A gente conhece os valores de pelo gráfico do enunciado, então podemos achar os valores de a partir desses caras.
Com isso o gráfico fica da seguinte maneira:
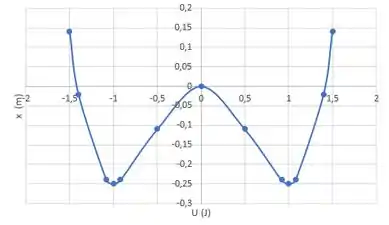
Passo 5
Agora vamos para o item .
Ele quer saber os pontos onde temos . No passo já vimos que:
Então para ser igual a zero temos que:
E para derivada ser zero os pontos devem ser pontos de máximo ou mínimo, ent]ao olhando o gráfico de vemos que isso acontece em , e em .
Passo 6
Agora vamos para a letra .
Agora temos que achar os intervalos onde temos positivo e negativo, já sabemos que:
Então vai ser positivo para valores negativos de . Isso quer dizer que os valores positivos de vão acontecer nos intervalos onde o gráfico de é decrescente.
E vai ser negativo para valores positivos de . Isso quer dizer que os valores negativos de vão acontecer nos intervalos onde o gráfico de é crescente.
Olhando o gráfico vemos que é positivo para e para .
E vai ser negativo para e para .
Passo 7
Agora finalmente o último, letra .
Quando soltamos a esfera de ela vai ter uma energia potencial inicial de que acaba sendo sua energia total, então ele só pode chegar a um ponto onde ele tenha a mesma energia total. Isso acontece em , então esse é o máximo que ela chega.
O maior valor de energia cinética vai ser quando ela tiver o menor valor de energia potencial, o menor valor de energia potencial que ela atinge nesse percurso é de olhando o gráfico.
Então o maior valor de energia cinética vai ser de , considerando que a energia total é de .
Com isso finalizamos essa questão com sucesso!
Resposta
A energia potencial é simétrica
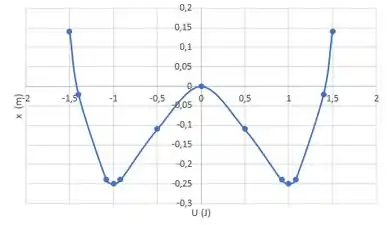
, e em
Positivo para e para .
Negativo para e para .
O maior valor é de .
O maior valor de energia cinética vai ser .