Enunciado
Física - Alaor Chaves- Ed: 1º - Capítulo 8.Exercícios e Problemas - Ex. 12
8.12E Uma bola de sinuca tem colisão elástica com outra bola idêntica e sofre um desvio de em sua trajetória. Que fração de sua energia cinética é transferida para a bola-alvo?
Passo 1
Belezoca galerinha, pra gente descobrir essa fração de energia cinética transferida, precisamos primeiro encontrar as velocidades finais de cada bola pra podermos comparar as energias cinéticas finais. Belezoca, só que a sagacidade aqui é que estamos tratando de corpos de massas iguais, e dessa forma entramos num caso de colisão em duas dimensões de acordo com a imagem:
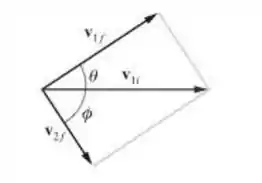
Onde no eixo , temos que:
Já para o eixo , devemos ter:
Sabemos que , maaassss a malandragem pra encontrar o valor de é que como a colisão é entre corpos de massas iguais, as velocidades finais devem ser ortogonais, tal que:
Logo:
De forma que nossas equações se tornam:
Passo 2
Show de bola, então se a gente substituir o valor das funções trigonométricas, obtemos:
E resolvendo esse sistema:
Logo a energia cinética inicial é:
Já a energia cinéica final da bola alvo é:
Dessa forma a fração de energia que a bola tranferiu para a bola alvo será:
Ou mais conhecido como o famosíssimo .