Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Alaor Chaves- Ed: 1º - Capítulo 8.Exercícios e Problemas - Ex. 4

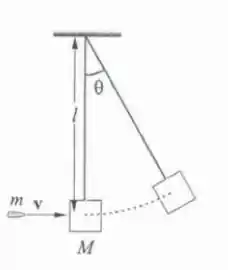
8.4P A figura 8.10 mostra um esquema do pêndulo balístico, que pode ser utilizado para medir a velocidade de um projétil, por exemplo uma bala. Esta, com massa m e velocidade v , atinge um bloco de massa M , suspenso por um fio, e fica incrustada nele. Observa-se o ângulo máximo θ alcançado pelo pêndulo. Calcule a velocidade v em função das outras variáveis do sistema.

Passo 1

Xuxu no mel galerinha, como estamos falando de uma colisão, podemos dizer que a energia mecânica total do sistema é conservada, tal que:

E i = E f

Maaaas, nosso projétil, antes de começar a subir no pêndulo, se choca com o bloco M se unindo a ele, tal que através da conservação do momento linear, vamos descobrir que a velocidade final do sistema bloco+projétil é:

m v = M + m v f

v f = m M + m v

Dessa forma a energia inicial que nosso sistema vai possuir antes de começar a escalar o pêndulo é:

E i = 1 2 M + m v f 2

E i = 1 2 M + m m M + m v 2

E i = 1 2 M + m m M + m 2 v 2

Já no momento final, no ponto mais alto do pêndulo, não possuimos velocidade, apenas energia potencial gravitacional, devido a altura alcançada pelo bloco+projétil, tal que:

E f = M + m g h

Onde h é a altura alcançada que por trigonometria podemos descobrir que é:

h = l - l cos ⁡ θ

h = l 1 - cos ⁡ θ

Passo 2

Belezera, dessa forma nossa conservação das energias fica assim:

1 2 M + m m M + m 2 v 2 = M + m g l 1 - cos ⁡ θ

Logo:

m M + m 2 v 2 = 2 g l 1 - cos ⁡ θ

v = M + m m 2 g l 1 - cos ⁡ θ

Resposta

v = M + m m 2 g l 1 - cos ⁡ θ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verdadeiro ou falso:A quantidade de movimento linear total de um sistema pode ser conservada mesmo quando a energia mecânica do sistema não o é.Para que a quantidade de movimento linear total de um si
Mostre que, se duas partículas têm a mesma energia cinética, então as magnitudes de suas quantidades de movimento são iguais apenas se elas têm a mesma massa.
A partícula A tem duas vezes a quantidade de movimento e quatro vezes a energia cinética da partícula B. Qual é a razão entre as massas das partículas A e B? Explique seu raciocínio.
Usando unidades SI, mostre que a razão entre as unidades do quadrado da quantidade de movimento e da massa é o joule.
Uma criança pula de um pequeno barco para o cais. Por que ela deve se esforçar mais neste caso do que se estivesse saltando de uma mesma distância, de cima de uma pedra para cima de um toco de árvore?