8.1E A figura 8.7 mostra um bloco na iminência de colidir com uma mola. Variação temporal da força de colisão é mostrada na figura 8.8. No instante , o bloco inicia o conato com a mola, e este contato se desfaz no instante . A função é dada por:
- Calcule o impulso dado ao bloco na colisão.
- Calcule a velocidade final do bloco.
- Calcule valor da força quando no ponto de retorno do bloco.

Passo 1
Belezera galerinha, queremos calcular o impulso que a mola fornece para o bloco na colisão. O gráfico da força exercida durante contado é dado por:
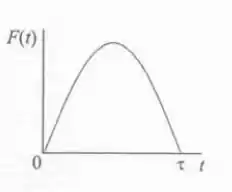
E através do gráfico podemos ver que a velocidade final do movimento será exatamente o inverso da velocidade inicial tal que:
E dito isso, sabemos que o impulso que uma força realiza sobre um corpo é dado plea variação do momento linear:
Passo 2
Iradoso, o momento linear inicial é dado por:
Já o momento linear final será:
Logo o impulso é dado como:
Passo 3
Meczada, na letra (B) já vimos no Passo 1 que . Já na letra (C), o enunciado nos pede pra calcular a força no ponto de retorno. Mas calma lá, porque o enunciado nos fez uma caridade e forneceu a equação da força, dada por:
Onde , e além disso sabemos que o tempo total da atuação da força é , só que a malandragem aqui é que não queremos o tempo total, e sim o tempo onde o bloco retorna seu movimento, que coincide exatamente com metade do tempo :
Portanto se a gente substituir esses valores na nossa equação, vamos obter:
E como , temos que:
E abrindo como :
Portanto o valor da força quando no ponto de retorno do bloco é: