Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 8.Problemas - Ex. 102
Um projétil de é disparado com velocidade de formando um ângulo de acima da horizontal. No ponto mais elevado de sua trajetória o projétil explode se dividindo em dois fragmentos de mesma massa, um dos quais cai verticalmente com velocidade inicial igual a zero. Despreze a resistência do ar. a) Supondo um solo horizontal, qual é a distância entre o ponto inicial do disparo e o ponto onde o segundo fragmento atinge o solo? b) Qual é a quantidade de energia libertada na explosão?
Passo 1
Fala, galerinha! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar (a) a distância entre o ponto inicial do disparo e o ponto onde o segundo fragmento atinge o solo e (b) a quantidade de energia libertada na explosão.
Vamos desenhar o que tá acontecendo pra gente entender melhor:
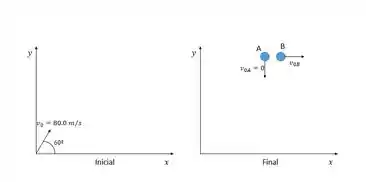
No primeiro plano, temos o projétil de massa e velocidade inicial sendo disparado com um ângulo de acima da horizontal. No segundo, temos o projétil sendo dividido em dois fragmentos, com o fragmento caindo verticalmente com velocidade inicial e o segundo fragmento , seguindo uma trajetória com velocidade .
Então, pra calcular a distância que o segundo fragmento alcança vamos usar a equação do movimento uniforme:
Onde é a distância alcançada (posição final), é a posição inicial do fragmento, sua velocidade inicial e é o tempo de queda. Só que pra determinar o tempo de queda e a nova velocidade do fragmento, vamos dividir o nosso movimento em duas partes e usar as equações de Torricelli e da conservação do momento linear do sistema.
Depois, vamos determinar a quantidade de energia liberada na explosão, considerando que ela é numericamente igual a variação de energia cinética do sistema ().
Vamos lá!
Passo 2
Quando o projétio é lançado a uma velocidade de com relação a horizontal, apenas nos interessa saber a que altura ele chegou, logo o distância na horizontal é desprezada inicialmente.
Desta forma temos que pela equação de Torritelli:
Onde aqui , que representa a aceleração da gravidade (), é a velocidade final, que é zero, é a velocidade inicial de lançamento e é a altura alcançada. Mas como o queremos a altura vertical, vamos considerar a componente vertical da velocidade inicial na direção . Sabendo que ela foi lançada com um ângulo de , temos:
Assim, isolando na equação, temos:
Passo 3
Atingindo a altura máxima, o projétio explode, dividindo em duas novas massas. Uma das massa fica parada no ar antes de começar a cair e a outra segue com uma nova velocidade. Pela conservação de momento temos que o momento linear inicial precisa ser igual ao final .
Para o momento inicial, temos:
Onde é a massa do projétil e é a componente horizontal da velocidade inicial ().
E o momento linear final vai ser dado pelo soma dos momento de cada fragmento. Como o projétil se divide em dois, temos nos dois fragmentos, velocidade zero para o primeiro (já que ele fica inicialmente parado no ar) e velocidade inicial para o segundo fragmento.
Traduzindo isso na equação, vamos ter:
Isolando temos que:
Simplificando:
Logo,
Passo 4
Agora que já temos a altura e a velocidade inicial do segundo fragmento, precisamos descobrir o tempo de queda dele.
Pra isso, vamos usar a equação do movimento uniformemente variado (MUV):
Como o tempo de queda para o primeiro e o segundo fragmento é o mesmo, consideramos , que é altura, a velocidade inicial e a posição final (que é o chão).
Assim, temos:
Isolando nessa equação, temos:
E substituindo e , vamos obter:
Passo 5
Agora analisando o movimento do segundo fragmento, vamos usar a equação:
Que implica em:
Então, a distância alcançada é dada por . Nós sabemos que e que . Assim, vamos ter:
Que é a distância entre o ponto inicial do disparo e o ponto onde o segundo fragmento atinge o solo.
Passo 6
Agora para calcular a Energia liberada na explosão, vamos calcular a energia cinética antes e depois da explosão .
A energia cinética inicial era de :
Substituindo a massa do projétil e , temos:
Da mesma forma, calculando a energia cinética final:
E substituindo os valores, ficamos com:
Logo, considerando a conservação de energia do sistema, temos que a energia liberada na explosão será dada por:
Valeu, galera! Até a próxima! 😉