Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 83
83. Um skatista parte com rapidez de de uma rampa de de altura e com de inclinação. As rodas do skate rolam sem atrito algum. A que distância do final da rampa o skatista toca a mesma?
Passo 1
Tudo bem senhores!? Aqui vamos nós de novo pra mais uma questãozinha de Cinemática!
E pra resolver esse tipo de questão, já sabe né?
Primeiro bora fazer um esboço pra ajudar a entender melhor o nosso problema...
De modo que obtemos então, a seguinte imagem abaixo...
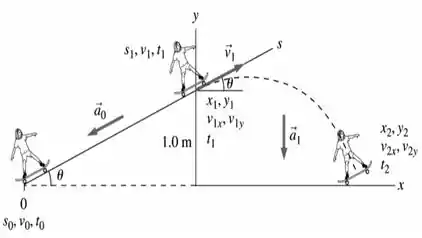
E pelo que sabemos dos problemas de movimento oblíquo e também do que lemos no enunciado, tiramos que...
Onde o objetivo aqui é encontrar a distância do final da rampa que o skatista toca, que pela figura, é o nosso !
Por isso, mãos à obra!
Passo 2
Bora pro que interessa! Chega de introdução!
Tomando como o instante inicial do movimento do skatista, vamos se concentrar inicialmente desde o intante em que ele entra na rampa até o momento em que ele sai dela. Nesse tempo, conforme colocamos em nossa figura, ele vai percorrer uma distância igual à...
Só que ele não executa um movimento uniforme. O skatista entra na rampa com uma velocidade e sai dela com outra velocidade, que no caso é bem menor!
Isso acontece devido ao fato de que a gravidade apesar de estar na vertical, tem uma componente na direção , onde está ocorrendo o movimento do skatisita na rampa. E essa componente vale...
Com sentido negativo, porque tem sentido contrário ao da trajetória... Voltando ao que interessa;
Bom! E como já temos a aceleração atuante, a velocidade inicial na entrada e o espaço percorrido pelo skatista; não vamos ser ingênuos, né!? Sem perder tempo, bora usar a famosa equação de Torricelli abaixo... Adaptando-a, é claro, às variáveis da nossa figura do ...
Substituindo os valores numéricos conhecidos;
Pronto! Essa é a velocidade com que o skatista sai da rampa!
Como ele sai da rampa com o mesmo ângulo que a rampa faz com a horizontal... Também não vamos perder tempo aqui, né parceiro(a)!?
Bora logo decompor essa velocidade rapaz...
Na direção horizontal:
E depois na vertical:
Passo 3
E como é de prache.. Pra facilitar a nossa resolução, bora dividir o movimento do skatista depois que sai da rampa, em duas partes; vertical e horizontal...
Na horizontal, em , nosso skatista não tem aceleração influenciando seu movimento. Sendo assim, ele executa um movimento uniforme, com velocidade constante.
Olhando pra nossa figura do , ficamos então com...
E substituindo os valores numéricos de cada variável;
Obtemos a equação que descreve o voo do skatista segundo a direção ...
Passo 4
Indo agora pra direção vertical, temos nessa direção a presença da aceleração da gravidade para baixo influenciando a trajetória da flecha.
Desse modo, peguemos a equação abaixo da posição para o movimento uniformemente variado... É claro, usando as variáveis da nossa figura, né!?
Esse é a nossa aceleração da gravidade , com sinal negativo porque aponta para baixo...
Ficamos então, com...
Logo; substituindo os valores conhecidos...
Obtemos a equação que descreve o movimento vertical!
E consequentemente, temos a seguinte equação para resolver...
Como é uma equação do grau no formato , basta usar a já conhecida fórmula abaixo...
Onde ficamos então, com as seguintes raízes abaixo...
E uma vez que só trabalhamos com tempo positivo, a única resposta possível para nossa equação é...
Passo 5
Obtido o tempo total do movimento do skatista desde que ele sai rampa; para obter a distância total percorrida pelo mesmo, basta recorrer à fórmula do ...
E substituindo o valor de :
Finalmente obtemos a nossa resposta!
Terminamos aqui! Até a próxima!