Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 12.Exercícios e Problemas - Ex. 75
As massas M e m estão ligadas por uma haste rígida, de massa desprezível e comprimento L. Elas giram em torno de um eixo perpendicular situado a uma distância x da massa M.
a. Para rotação com velocidade angular !, para que valor de x esse haltere giratório possui energia de rotação mínima?
b. Qual é o significado físico deste valor de x?
Passo 1
As massas são partículas.
Vamos visualizar a situação:
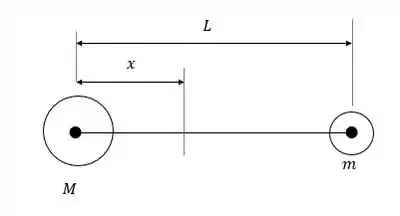
Passo 2
- O momento de inércia da barra é
- Este é o centro da localização da massa medida a partir da massa M.
A energia cinética rotacional é portanto
Para encontrar de modo que a seja mínima, definimos:
Passo 3
Resposta
- centro da localização da massa medida a partir da massa M
Exercícios de Livros Relacionados
Desejamos armazenar energia em um volante de 70,0 k g que possui forma de um disco maciço uniforme com raio R = 1,20 m . Para imperir danos estruturais, a aceleração radial máxima de um ponto na sua p
Fator de escala de I . Quando multiplicamos todas as dimensões de um objeto por um fator de escala f , sua massa e seu volume ficam multiplicados por f 3 . a) O momento de inércia ficará multiplicado
Um volante de motor a gasolina deve fornecer uma energia cinética igual a 500J , quando sua velocidade angular diminui de 650r e v / m i n para 520r e v / m i n . Qual é o momento de inércia necessári
Suponha que o cilindro maciço do dispositivo descrito no Exemplo 9.9 (Seção 9.4) seja substituído por uma casca cilíndrica com o mesmo raioR e com a mesma massa M . O cilindro é ligado ao eixo por mei
Você deve projetar uma plataforma giratória industrial com 60,0c m de diâmetro e energia cinética de 0,250J quando gira a 45,0r p m( r e v / m i n ) . a) Qual deve ser o momento de inércia da platafor