Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 24.5 - Ex. 8
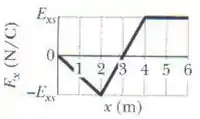
A abaixo mostra um gráfico da componente x do campo elétrico em função de x em uma certa região do espaço. A escala do eixo vertical é definida por = 20,0 N/C. As componentes y e z do campo elétrico são nulas em toda a região. Se o potencial elétrico na origem é 10 V, (a) qual é o potencial elétrico em x = 2,0 m? (b) Qual é o maior valor positivo do potencial elétrico em pontos do eixo x para os quais ? (c) Para que valor de x o potencial elétrico é zero?
Passo 1
Letra (a)
Gente, pra calcular a diferença de potencial, existe essa fórmula:
Mas isso é a mesma coisa que pegar a área de um gráfio CAMPO ELÉTRICO X POSIÇÃO, que é exatamente o gráfico acima.
Passo 2
Para x = 2, vamos calcular o negativo da área entre 0 e 2:
Daí,
Passo 3
Letra (b)
Veja bem: A gente que pegar o máximo da integral. Só que a integral é o negativo da área. Só que a área começa negativa, e depois fica positiva. Só que o negativo do negativo é positivo e o negativo do positivo é negativo. Então a gente quer qual parte da área? A negativa, certo? Porque quando jogar na integral ela vai ficar positiva. Então a gente vai pegar a entre x = 0 e x = 3 m
Passo 4
Passo 5
Letra (c)
Você percebeu que de zero até 3 m deu 40 V? Então agora a gente tem que pegar a área positiva (depois de x = 3 m) porque aí a área positiva vai ficar negativa e vai cancelar aqueles 40 V que a gente achou.
Passo 6
Vamos calcular a área positiva (que vai ficar negativa na integral)
- De x = 3m a x = 4m
- De x = 4m a algum ponto x
Área do retângulo:
Passo 7
A soma das duas áreas tem que dar -40 (pra cancelar o 40 V que a gente achou no item b):
Resposta
Letra (a):
Letra (b):
Letra (c):