(a) Se a aceleração máxima que pode ser tolerada pelos passageiros de um metrô é e duas estações de metrô estão separadas por uma distância de , qual é a velocidade máxima que o metrô pode alcançar entre as estações? (b) Qual é o tempo de percurso? (c) Se o metrô para durante em cada estação, qual é a máxima velocidade escalar média do metrô entre o instante em que parte de uma estação e o instante em que parte da estação seguinte? Plote , e em função de para intervalo de tempo entre o instante em que o trem parte de uma estação e o instante em que parte da estação seguinte.

Bom pessoal, o tempo gasto para a velocidade sair do até com uma aceleração de é o mesmo para a velocidade sair de até o com uma aceleração de , concordam? Dessa forma só precisamos calcular um deles e multiplicar por dois para acharmos o tempo total do percurso . Temos que :

Tranquilo até aqui , pessoal?

Então galera, nesse caso só precisamos considerar o tempo de que foi perdido nesse intervalo :

Agora podemos calcular a velocidade média normalmente usando a relação :

Então pessoal , antes de esboçarmos o gráfico temos que pensar em como será sua aparência . Bora começar pelo gráfico da posição em função do tempo . Temos que :

Reparem que é uma função do segundo grau com coeficiente angular , cujo gráfico nós sabemos que pode ser descrito por uma parábola . A posição parte do e , inicialmente , como a concavidade da parábola estará para cima . Quando , a posição continua aumentando , uma vez que a velocidade ainda é positiva, porém a concavidade da parábola estará para baixo . Quando a velocidade chega no o trem para dedesacelerar , e velocidade permanece nula por segundos , ou seja , a posição não varia . Sendo assim :

Tranquilo galera ? Bora para o próximo então!

Agora podemos pensar em como o gráfico da velocidade se comporta. Temos que :

Reparem que é uma função do primeiro grau com coeficiente angular que nos indica o quanto a componente aumenta em função do acréscimo de unidade da componente .Sabemos que o gráfico de uma função de primeiro grau é descito por uma reta e quando a reta é crescente , quando a reta é decrescente e quando a função é constante . Sendo assim :

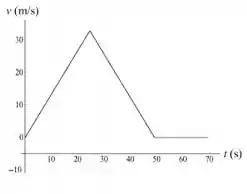
Tranquilo ? Agora o último é o mais de boa .

Para acharmos gráfico da aceleração temos que perceber que nesse caso ela não está em função de nenhuma variável , logo , será sempre constante . Sendo assim :

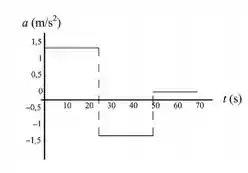
Tranquilo galera? Bora resolver mais questões então!!!!!