Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 2.10 - Ex. 66
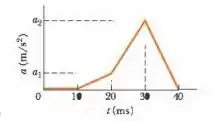
Uma salamandra do gênero Hydromantes captura a presa lançando a língua como um projétil: a parte traseira da língua se projeta bruscamente para a frente, desenrolando o resto da língua até que a parte dianteira atinja a presa, capturando-a. A Fig. 2-36 mostra o módulo de aceleração em função do tempo durante a fase de aceleração em uma situação típica. As acelerações indicadas são e Qual é a velocidade da língua no final da fase de aceleração?
Passo 1
Para começar vamos lembrar a definição de velocidade:
,
sem esquecer que a integral é a área da função que estamos integrando.
O exercício nos deu o gráfico da aceleração. Então, para calcular a velocidade da língua no final da fase da aceleração, basta calcularmos a área do gráfico.
Porém, precisamos prestar atenção nas unidades do problema. O eixo da aceleração (eixo ) está em e o eixo do tempo (eixo ) está em , logo, precisamos consertar as unidades. Para isso, multiplicaremos o eixo do tempo por para transformar de milissegundo para segundo.
Para resolução de problemas como este, o macete é separar o gráfico em figuras com as fórmulas de áreas conhecidas. As fórmulas das áreas figuras que aparecem neste exercício são:
Passo 2
Para esta questão, vamos calcular a área de 3 figuras, sendo dois triângulos e um trapézio:
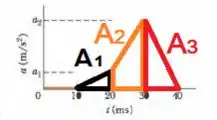
Primeira divisão (triângulo preto):
Segunda divisão (trapézio laranja):
Terceira divisão (triângulo vermelho):
Assim, para encontrar a velocidade da língua no final da fase da aceleração basta somar as áreas calculadas acima: