Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 8.Problemas - Ex. 12
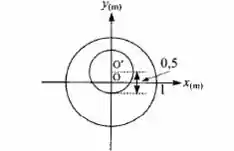
Calcule as coordenadas do CM da placa homogênea indicada na figura, um círculo de 1m e de raio do qual foi removido um círculo de 0,5 m de raio, com uma separação de 0,25m entre os centros O e O’ dos dois círculos.
Passo 1
Galera, pra calcular isso aqui com as integrais dá um trabalhinho, por isso vamos usar a famosa malandragem, hehe. O segredo é considerar a placa maior inteira e a menor com massa negativa. Cola aqui pra ver como é
- Placa maior tem centro de massa em O por sua simetria, logo
- Placa menor está deslocada na vertical
Estabelecemos essa proporcionalidade já que as placas são homogêneas
Resposta
Exercícios de Livros Relacionados
Na Fig. 9-37, três barras finas e uniformes, de comprimento L = 22c m , formam um U invertido. Cada barra vertical tem uma massa de 14g ; a barra horizontal tem massa de 42g . Quais são (a) a coordena
Uma partícula de 2,00k g tem coordenadas x y ( - 1,20m , 0,500m ) e uma partícula de 4,00k g tem coordenadas x y ( 0,600m , - 0,750m ). Ambas estão em um plano horizontal. Em que coordenada (a) x e (b
A Fig. 9-36 mostra uma placa composta de dimensões d 1 = 11,0c m , d 2 = 2,80c m e d 3 = 13,0c m . Metade da placa é feita de alumínio (massa especifica = 2,70g / c m 3 ) e a outra metade de ferro (ma
A Fig. 9-39 mostra uma caixa cúbica que foi construída com placas metálicas uniformes de espessura desprezível. A caixa não tem tampa e tem uma aresta L = 40c m . Determine (a) a coordenada x , (b) a
Na Seção 8.5 calculamos o centro de massa considerando objetos compostos por um número finito de massas puntiformes ou objetos que por simetria pudessem ser representados por um número finito de massa