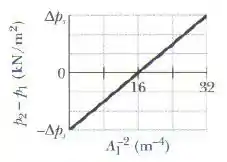
Água doce escoa horizontalmente do segmento de uma tubulação, com uma seção reta , para o segmento , com uma seção reta . A figura mostra um gráfico da relação entre a diferença de pressão em função do inverso do quadrado da área que seria esperada para uma vazão de certo valor se o escoamento fosse laminar em todas as circunstâncias. A escala do eixo vertical é definida por. Nas condições da figura, quais são os valores (a) de e (b) da vazão?

Como o gráfico do enunciado está em função de , vamos usar a equação da continuidade para tentar substituir isso na fórmula que acabamos de achar.

Isso permite dizer que:

Substituindo isso na fórmula que encontramos pela equação de Bernoulli:

E chegamos na função:

Pronto, essa é uma função de em função de , ou seja, é exatamente a função que está representada no gráfico.

Se chamarmos de o coeficiente angular da reta, e de o coeficiente linear, dá pra ver pela equação da reta que:

E

Sabemos que o coeficiente angular pode ser identificado no gráfico pelo ponto em que a reta cruza o eixo , nesse caso:

Agora olhe para o ponto em que a reta cruza o eixo , isso acontece no ponto , substituindo isso na nossa função:

E essa é a resposta da letra (a).

Agora, a letra (b) quer saber a vazão da tubulação. Vamos ver a fórmula para isso:

Como já sabemos e , vamos usar o último termo da igualdade:

Pronto!