Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 56
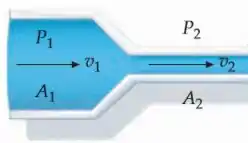
A pressão em uma seção de um cano horizontal de 2,00 cm de diâmetro é de 142kPa. Água escoa através do cano a 2,80 L/s. Se a pressão em um certo ponto é reduzida a 101 kPa, devido a um estrangulamento de uma seção do cano, qual deve ser o diâmetro da seção estrangulada?
Passo 1
Falaa, querido! Temos um tubo onde há um estrangulamento (redução da seção transversal). Ele quer saber o diâmetro da seção depois desse estrangulamento para que a pressão passe a ser de .
A ideia aqui é a gente analisar dois pontos. O ponto 1, que fica antes do estrangulamento, e o ponto 2 que fica depois.
No ponto 1, temos os seguintes dados
No ponto 2
E tem dados que valem para os dois pontos. Temos a massa específica da água que vale
E a vazão volumétrica, que como água é incompressível, vai ser a mesma em todos os pontos
Para questões assim com fluxo e um estrangulamento, temos duas fórmulinhas uteis. A da vazão
E a de Bernoulli
A ideia é usar esses dados e essas fórmulinhas para achar . Vamos!
Passo 2
Meus consagrados, inicialmente, iremos fazer uso da equação da continuidade, dada por:
Ela diz que a vazão é sempre a mesma, não importa o ponto. Substituindo a fórmula da vazão
Onde:
e são as áreas das seções transversais em no ponto 1 e no ponto 2;
e são as velocidades de fluxo nos respectivos pontos.
Para prosseguirmos, precisaremos lembrar de uma coisinha, já que iremos considerar as seções como sendo circulares:
Como consequência disso:
Tal que:
Então:
Já sabemos :
Passo 3
Notem que ainda possuímos 3 incógnitas: , para tentarmos eliminá-las, vamos tentar entrelaçar algumas equações para facilitar nossa vida!!!
Vamos tentar eliminar da nossa equação.
Usando a fórmula da vazão em 1:
Vimos que para qualquer ponto, e já sabemos quem é :
Isolando :
Passo 4
Por último, iremos usar a equação de Bernoulli para eliminar
Notem que a questão nos informa que ambas as extremidades estão à mesma altura, logo portanto podemos cancelar a expressão de ambos os lados da equação e passamos a ter:
Como queremos eliminar , vamos isolá-lo, meus amigos:
Vamos substituir nossos dados:
Passo 5
Finalmente, agora a gente acha . Lembra que achamos que
Substituindo os valores que achamos para as velocidades