Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 13.1 - Ex. 59

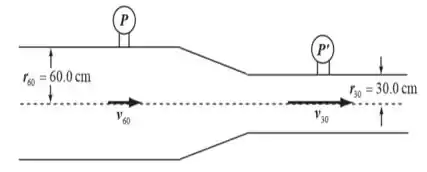
O gasoduto do Alaska tem uma vazão máxima de I v = 240.000 m 3 / d , sabendo que a maior parte do tubo tem raio r 60 = 60,0 c m , encontre a pressão P ' em um ponto de raio r 30 = 30,0 c m , considerando a pressão no ponto de raio r 60 como sendo P = 180 k P a , p = 800 k g / m 3 . Assumindo um fluxo laminar não viscoso de estado estacionário.

Passo 1

Iremos usar a equação de Bernoulli para achar as relações de P 1 e P 2 :

P + p g h 1 + 1 2 p v 60 2 = P ' + p g h 2 + 1 2 p v 30 2

Notem que a questão nos informa que ambas as extremidades estão à mesma altura, portanto podemos cancelar a expressão p g h de ambos os lados da equação e passamos a ter:

P + 1 2 p v 60 2 = P ' + 1 2 p v 30 2

Como queremos saber P ' , vamos isolá-lo na equação:

P ' = P + 1 2 p v 60 2 - 1 2 p v 30 2

P ' = P + 1 2 p ( v 60 2 - v 30 2 )

Passo 2

Notem que temos muitas variáveis desconhecidas v 60 e v 30 , portanto, iremos tentar correlacioná-las para facilitar nossa vida!!!

Usando a definição temos:

I v = A v

v 60 = I v A 60

v 60 = I v π r 60 2

Passo 3

Agora usando a equação da continuidade, temos:

A 60 v 60 = A 30 v 30

Isolando v 30 :

v 30 = v 60 A 60 A 30

Passo 4

Agora, vamos entrelaçar as equações:

P ' = P + 1 2 p ( v 60 2 - v 30 2 )

v 60 = I v π r 60 2

v 30 = v 60 A 60 A 30

Para facilitar nossa parte algébrica, vamos substituir, primeiramente, v 60 em v 30 :

v 30 = v 60 A 60 A 30

v 30 = I v π r 60 2 A 60 A 30

Tal que:

A 60 = π r 60 2

Logo, podemos simplificar:

v 30 = I v A 30

Agora, iremos para a equação que vai nos dar o resultado:

P ' = P + 1 2 p ( v 60 2 - v 30 2 )

P ' = P + 1 2 p ( I v π r 60 2 2 - I v π r 30 2 2 )

P ' = P + p I v 2 2 π 2 ( 1 r 60 4 - 1 r 30 4 )

Observação: 1dia=1.24h=1.24.60min=1.24.60.60s

Por fim, vamos substituir os valores fornecidos:

P ' = 180.10 3 + 800 . 24.10 4 . 1 24 1 60 1 60 2 2 π 2 ( 1 0,6 4 - 1 0,3 4 )

P ' = 180.10 3 - 36,286.10 3

P ' = 144.10 3 P a

P ' = 144 k P a

Resposta

P ' = 144 k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Você usa a broca para fazer um pequeno furo na lateral de um tanque cilíndrico vertical de água assentado sobre o solo com seu topo aberto para o ar. (a) Se o nível da água tiver uma altura H, em que
Um tanque cilíndrico vertical de área de seção reta A 1 está aberto para o ar em seu topo e contém água até a profundidade h o . Um empregado abre acidentalmente um furo de área A 2 no fundo do tanque
O furacão Emily, ocorrido em 1993, apresentava um raio de aproximadamente 350 km. A velocidade do vento ao redor do vcentro (o “olho”) do furacão, de raio 30 km, atingiu 200 km/h. À medida que o ar fo
Um balde cilíndrico, aberto na parte superior, possui diâmetro de 10,0 cm e altura igual a 25,0 cm. Um orifício circular com área da seção reta igual a 1,50 c m 2 é feito no centro da base do balde. A
Dois grande tanques abertos A e F (Figura 14.44) contém o mesmo liquido. Um tubo horizontal BCD, que tem uma constrição C e é aberto ao ar no ponto D, sai da base do tanque A, e um tubo vertical E par