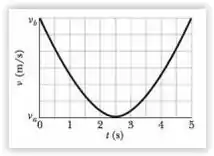
Uma bola de golfe recebe uma tacada no solo. A velocidade da bola em função do tempo é mostrada na Fig. 4 -36, onde é o instante em que a bola foi golpeada. A escala vertical do gráfico é definida por e .

(a) Que distância horizontal a bola de golfe percorre antes de tocar novamente o solo?

(b) Qual é a altura máxima atingida pela bola?

Então galera, o movimento como um todo pode ser dividido em movimento uniforme em relação ao eixo e movimento uniformemente variado em relação ao eixo . No instante , onde ocorre a velocidade mínima, podemos concluir que a componente vertical da velocidade é nula e, dessa forma, o módulo da velocidade nesse ponto é o mesmo da componente horizontal da velocidade, uma vez que:

Logo:

A bola tocará o solo com a mesma velocidade que foi gopeada inicialmente, sendo assim, o instante em que isso acontece é dado pelo gráfica e vale . Como o movimento horizontal é uniforme, ou seja, com velocidade constante, podemos achar a distância horizontal atingida pela bola através da relação: