Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 3.Problemas - Ex. 56
Uma mangueira de água é usada para encher um grande tanque cilíndrico com diâmetro e altura . O jato de água sai da mangueira a acima da horizontal, a partir do mesmo nível da base do tanque, e está a uma distância (Figura ). Para qual alcance de velocidade de lançamento () a água entrará no tanque? Despreze a resistência do ar e expresse sua resposta em termos de e .
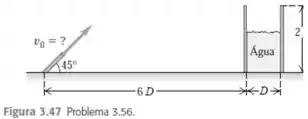
Passo 1
Show de bolinhas pessoal? Vamos analisar a situação!
Como a mangueira joga água a partir do chão com uma velocidade inicial que faz um ângulo com a horizontal, a água descreve um lançamento obliquo, olha só:
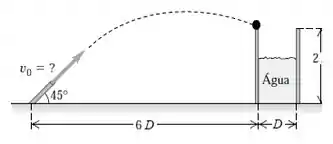
Então as equações do movimento em cada eixo, serão:
A água entra no tanque com passando pelo primeiro ponto sinalizado na figura! Repara que nesse ponto, temos as coordenadas:
Além disso, o problema nos informa que , logo:
Calculando,
Show de bola!!
Passo 2
Agora, o tempo para atingir esse ponto, podemos encontrar a partir da primeira equação, tal que:
Ou seja:
E na vertical:
Agora substituindo o tempo na expressão ali de cima temos:
Uma equação só pra :
Portanto:
Tranquilo até aqui?
Passo 3
Agora vamos fazer o mesmo procedimento, mas agora para a posição máxima onde o jato de água ainda atinge o tanque:
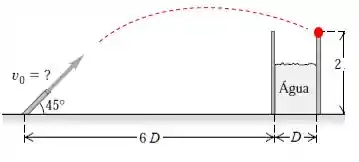
Onde esse ponto é dado pelas coordenadas:
Sendo assim, começamos pelo tempo para atingir a maior distância, que é dado como:
Ou seja:
E na vertical:
Agora substituindo o tempo na expressão ali de cima temos:
Uma equação só pra :
Então o intervalo de velocidades é:
E então! O que achou? Responde Aí!
