Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Príncipios de física - Serway - Princípios De Física: Mecânica Clássica e Relatividade - Ed: 5º - Capítulo 3.Problemas - Ex. 52

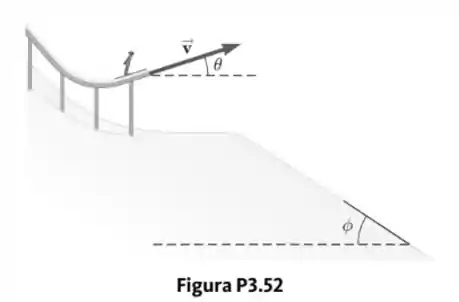
Uma esquiadora sai de uma rampa de esqui com velocidade de v   =   10,0   m / s em θ   =   15,0 ° acima da horizontal, como mostrado na Figura P3.52. A encosta onde ela vai pousar é inclinada para baixo em ϕ   =   50,0 ° , e a resistência do ar é desprezível. Encontre

  1. a distância entre a extremidade da rampa onde a saltadora pousa e
  2. as componentes de sua velocidade antes do pouso.
  3. Explique por que os resultados poderão ser afetados se a resistência do ar for incluída.

Passo 1

E aiii gente, tudo bom com vocês?

Vamos fazer mais uma questãozinha aqui?

Vem comigo!

Letra a:

Medido a partir do final da rampa, o esquiador pousa a uma distância d abaixo do declive no tempo t:

Δ x = v x t → d c o s ⁡ 50.0 ∘ = ( 10.0 m / s ) cos ⁡ 15.0 ∘ t

E

Δ y = v y y t + 1 2 g t 2 → - d s i n ⁡ 50.0 ∘ = ( 10.0 m / s ) sin ⁡ 15.0 ∘ t + 1 2 - 9.80 m s 2 t 2

Resolvendo temos d = 43.2 m   e   t = 2.88 s .

Passo 2

Letra b:

Como a x = 0 :

v x f = v x i = ( 10.0 m / s ) c o s ⁡ 15.0 ∘ = 9.66 m / s v y f = v y i + a y t = ( 10.0 m / s ) s i n ⁡ 15.0 ∘ - 9.80 m s 2 ( 2.88 s ) = - 25.6 m / s

Passo 3

Letra c:

A resistência do ar normalmente diminuiria os valores da faixa e velocidade de pouso. Ela pode desviar o ar para baixo de modo que o ar a desvia para cima. Isso significa que ela pode se levantar um pouco e aumentar sua distância.

Resposta

  1. d = 43.2 m  e  t = 2.88 s .
  2. - 25.6 m / s
  3. A resistência do ar normalmente diminuiria os valores da faixa e velocidade de pouso. Ela pode desviar o ar para baixo de modo que o ar a desvia para cima. Isso significa que ela pode se levantar um pouco e aumentar sua distância.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O alcance de um projétil é 4 vezes sua altura máxima, e ele permanece no ar durante 2s. a) em que ângulo ele foi lançado ? b) Qual foi a velocidade incial ? c) Qual é o alcance ?
Um canhão lança um projétil por cima de uma montanha russa de altura h, de forma a passar quase tangenciando o cume C no ponto mais alto da sua trajetória. A distância horizontal entre o canhão e o cu
Um jogador de futebol, a 20,5 m do gol adversário, levanta a bola com um chute a uma velocidade inicial de 15m/s, passando-a ao centroavante do time, que está alinhado com ele o gol a 5,5 m do gol. O
Um jogador de futebol inexperiente chuta um pênalti a 9m do gol, levantando a bola com velocidade inicial de 15 m/s. A altura da trave é de 2,4m. Calcule: a) a que distância máxima da trave, atrás do
Generalize o resultado do problema anterior, mostrando que um projétil lançado do chão com uma velocidade inicial v 0 pode atingir um ponto situado à distância x e à altura y para dois ângulos de elev