Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 3.1 - Ex. 79
A de sua altura máxima, a rapidez de um projétil é de sua rapidez inicial. Qual foi o ângulo de lançamento? (Ignore a resistência do ar.)
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
A figura abaixo retrata o movimento do enunciado:
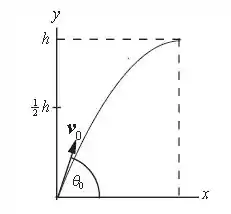
O problema nos pede o ângulo de lançamento a partir das informações dadas:
Como a velocidade no ponto de altura máxima é nula, temos:
Aplicando o nosso problema temos que:
Sabemos que:
Logo:
Passo 2
O ângulo de lançamento é dado por:
Resposta
Exercícios de Livros Relacionados
Um mergulhador salta com uma velocidade horizontal de 2,00m / s de uma plataforma que está 10,0m acima da superfície da água.(a) A que distância horizontal da borda da plataforma está o mergulhador 0,
Uma pedra é lançada por uma catapulta no instante t= 0 , com uma velocidade inicial de módulo 20,0m / s e ângulo 40,0 ° acima da horizontal. Quais são os módulos das componentes (a) horizontal e (b) v
Um arremessador de peso de nível olímpico é capaz de lançar o peso com uma velocidade inicial v 0 = 15,00m / s de uma altura de 2,160m . Que distância horizontal é coberta pelo peso se o ângulo de lan
Na Fig. 4 -37, uma bola é lançada para a esquerda da extremidade esquerda do terraço de um edifício. O ponto de lançamento está a uma altura h em relação ao solo e a bola chega ao solo 1,50s depois, a
Durante uma partida de tênis, um jogador saca a 23,6m / s , com o centro da bola deixando a raquete horizontalmente a 2,37m de altura em relação à quadra. A rede está a 12m de distância e tem 0,90m de